
1. 理论分析
此处使用均方误差作为回归任务的性能度量,均方误差公式为:
\[E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^2\]均方误差的意义为:欧几里得距离,即“欧氏距离”
我们可以使用最小二乘法来求解模型(最小二乘法指的是基于均方误差最小化求解模型的方法):
\[\begin{align} (w^*,b^*)&=\arg\max_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2\\ &=\arg\max_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2 \end{align}\]最小二乘法的意义为:试图找到一条直线,使所有样本到直线的欧氏距离最小
求解$w,b$使$E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2$最小化的过程,称为线性参数模型最小二乘“参数估计”:
- 先求导
- 令导数为 0,求解$w,b$最优解
此处$\cfrac{1}{m}\sum_{i=1}^{m}y_i=\bar{y}$,$ \cfrac{1}{m}\sum_{i=1}^{m}x_i=\bar{x} $
2. 代码实现
第一步:数据预处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset = pd.read_csv('datasets/studentscores.csv')
X = dataset.iloc[ : , : 1 ].values
Y = dataset.iloc[ : , 1 ].values
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size = 1/4, random_state = 0)
第二步:训练集使用简单线性回归模型来训练
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor = regressor.fit(X_train, Y_train)
第三步:预测结果
Y_pred = regressor.predict(X_test)
第四步:可视化
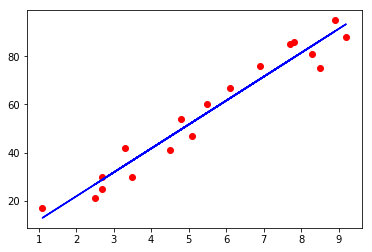
训练集结果可视化
plt.scatter(X_train , Y_train, color = 'red')
plt.plot(X_train , regressor.predict(X_train), color ='blue')
plt.show()
测试集结果可视化
plt.scatter(X_test , Y_test, color = 'red')
plt.plot(X_test , regressor.predict(X_test), color ='blue')
plt.show()
