1. 非线性激活函数的必要性
如果使用线性激活函数(恒等激励函数),那么神经网络仅是将输入线性组合再输出,在这种情况下,深层(多个隐藏层)神经网络与只有一个隐藏层的神经网络没有任何区别,不如去掉多个隐藏层。
证明如下:
\[a^{[1]}=z^{[1]}=W^{[1]}x+b^{[1]}\\ a^{[2]}=z^{[2]}=W^{[2]}x+b^{[2]}=W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}\\ a^{[2]}=z^{[2]}=W^{[2]}W^{[1]}+W^{[2]}b^{[1]}+b^{[2]}\\ 简化得:a^{[2]}=z^{[2]}=W^`x+b\]如上公式,两层使用线性激活函数的神经网络,可以简化成单层的神经网络,对于多个隐藏层的神经网络同样如此。因此,想要使神经网络的多个隐藏层有意义,需要使用非线性激活函数,也就是说想要神经网络学习到有意思的东西只能使用非线性激活函数。
下面将介绍各个激活函数
2. sigmoid(logistic回归使用的激活函数)
公式:
\[a=g(z)=\frac{1}{1+e^{-z}}\]绘制函数图像代码:
#导入相关库
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:1/(1+np.exp(-x))
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='sigmoid')
plt.grid(True)#显示网格
plt.legend()#显示旁注#注意:不会显示后来再定义的旁注
plt.show(fig)
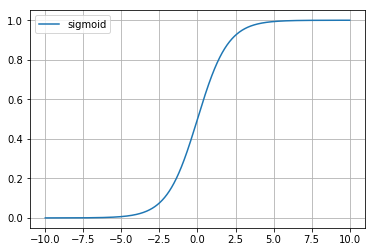
函数图像:

由图像可知,sigmoid函数的值域为(0,1)
导数:
\[g^`(z)=g(z)*(1-g(z))\]3. tanh
公式:
\[a=g(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\]绘制函数图像代码:
#导入相关库
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:(np.exp(z)-np.exp(-z))/(np.exp(z)+np.exp(-z))
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='tanh')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
函数图像:
由图像可知,tanh函数是sigmoid函数向下平移和收缩后的结果。
导数:
\[g^`(z)=1-(g(z))^2\]sigmoid和tanh激活函数有共同的缺点:即在z很大或很小时,梯度几乎为零,因此使用梯度下降优化算法更新网络很慢。
4. relu(修正线性单元)
公式:
\[a=g(x)=\max(0,z)\]绘制函数图像代码:
#导入相关库
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:np.maximum(0,z)
start=-10 #输入需要绘制的起始值(从左到右)
stop=10 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='relu')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
函数图像:

导数:
\[g^`(z)=\begin{cases} 1 & \text {if z > 0} \\ undefined & \text {if z=0}\\ 0 & \text {if z<0}\\ \end{cases}\]由于sigmoid和tanh存在上述的缺点,因此relu激活函数成为了大多数神经网络的默认选择。
但是relu也存在缺点:即在$z$小于0时,斜率即导数为0,因此引申出下面的leaky relu函数,但是实际上leaky relu使用的并不多。
5. Leaky relu
公式:
\[a=g(x)=\max(0.01z,z)\]绘制函数图像代码:
#导入相关库
import matplotlib.pyplot as plt
import numpy as np
#函数
g=lambda z:np.maximum(0.01*z,z)
start=-100 #输入需要绘制的起始值(从左到右)
stop=50 #输入需要绘制的终点值
step=0.01#输入步长
num=(stop-start)/step #计算点的个数
x = np.linspace(start,stop,num)
y = g(x)
fig=plt.figure(1)
plt.plot(x, y,label='relu')
plt.grid(True)#显示网格
plt.legend()#显示旁注
plt.show(fig)
函数图像:

导数:
\[g^`(z)=\begin{cases} 1 & \text {if z > 0} \\ undefined & \text {if z=0}\\ 0.01 & \text {if z<0}\\ \end{cases}\]