1. 引言
当我们训练一个深层神经网络时,可能存在过拟合和欠拟合的情况,而我们想要的一个状态是存在于欠拟合和过拟合之间的一个点,即偏差小方差也小。
但是如果如果我们的模型过拟合怎么办呢?
事实上有两种解决办法比较通用,一种是准备更多的数据,但是实际上却不容易实现;另一种就是今天的主角,使用正则化方法。
在接下来的内容中,我们会先给出对应的正则化方法的公式与使用方法,然后再对正则化方法为何能够防止过拟合做一个形象的解析。
Begining~
2. L2正则化方法
首先介绍向量的欧几里得范数,也叫作2范数:
\[\|\textbf w\|^2_2=\sum_{j=1}^{n_x}w_j^2=\textbf w^T\textbf w \tag{2-1}\]实际意义为向量中每个元素的平方和,然后介绍矩阵的弗罗贝尼乌斯范数,用下标F标注:
\[\|\textbf w^{[l]}\|_F^2 = \sum_{i=1}^{n^{[l]}}\sum_{j=1}^{l^{[l-1]}}(w_{ij}^{[l]})^2 \tag{2-2}\]上式的实际意义为求解矩阵中所有元素的平方和。
使用L2范数后成本函数中的正则项为:
\[\frac{\lambda}{2m}\sum_{l=1}^L\|\textbf w^{[l]}\|^2=\frac{\lambda}{2m}\sum_{l=1}^L\sum_{i=1}^{n^{[l]}}\sum_{j=1}^{l^{[l-1]}}(w_{ij}^{[l]})^2 \tag{2-3}\]公式2-3是完整的正则项公式,我们将其加入到成本函数中:
\[J(\textbf w,b)=\frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}\sum_{l=1}^L\|\textbf w^{[l]}\|^2 \tag{2-4}\]公式2-4就是使用L2正则化后的完整的成本函数了,其实本质上就是原成本函数的后面加上了正则项,但是这个正则项具体是怎样影响到权值更新呢,我们来看一下反向传播的过程:
我们使用BP表示未加L2正则项的成本函数对应的梯度,那么我们的梯度下降公式为:
\[d\textbf w^{[l]}=BP+\frac{\lambda}{m}\textbf w^{[l]}\\ \begin{align} \textbf w^{[l]}&:=\textbf w^{[l]}-\alpha d\textbf w^{[l]}\\ &:=\textbf w^{[l]}-\alpha(BP+\frac{\lambda}{m}\textbf w^{[l]})\\ &:=\textbf w^{[l]}-\frac{\alpha\lambda}{m}\textbf w^{[l]}-\alpha BP\\ &:=(1-\frac{\alpha\lambda}{m})\textbf w^{[l]}-\alpha BP \end{align}\tag{2-5}\]公式2-5是反向传播过程中,带有L2正则化参数更新过程,从最后的结果来看,相对比未使用L2正则化的更新过程,L2正则化相当于减小参数$\textbf w$的值,相当于$\textbf w$乘以$(1-\frac{\alpha\lambda}{m})$的权重($(1-\frac{\alpha\lambda}{m})<1$).
还是提及一下L1正则化,虽然大多数人都在用L2正则化。
L1正则化其实和L2正则化很是类似,不同点在于L2正则化使用的是每个权重值的平方和,而L1正则化使用每个权重值的绝对值的和。
仅列出L1正则化的公式:
\[\frac{\lambda}{2m}\|\textbf w\|_1=\frac{\lambda}{2m}\sum_{j=1}^{n_x}|w_j|\tag{2-6}\]使用L1正则化后,参数会稀疏,即参数中有很多0。
L1正则化可通过假设权重w的先验分布为拉普拉斯分布,由最大后验概率估计导出。
L2正则化可通过假设权重w的先验分布为高斯分布,由最大后验概率估计导出。
3. 直观理解L2正则化
我们从两个角度直观的理解L2正则化能够预防过拟合的原因:
1. 从网络的复杂度
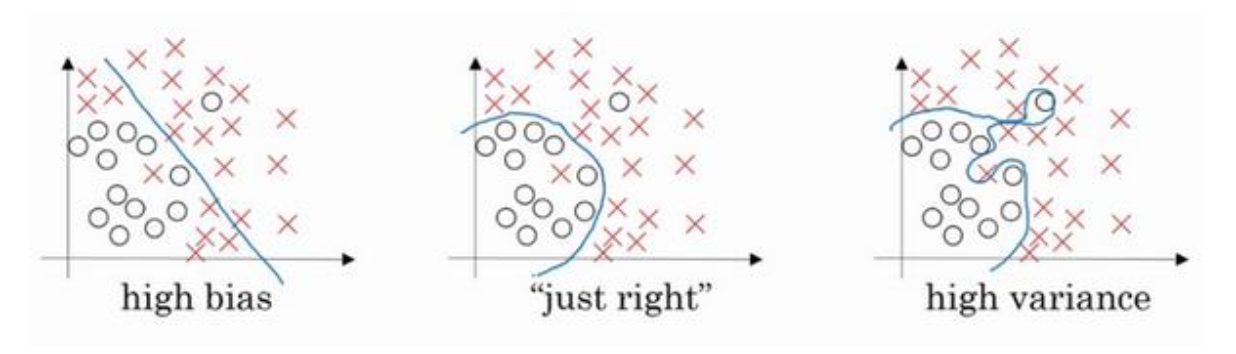
上图中,左图为欠拟合状态,中间为最合适的状态,右图为过拟合状态。
我们可以发现随着模型的复杂度过高,容易发生过拟合。
在使用L2正则化后,按照公式2-5所示,超参数$\lambda$设置的越大,参数$\textbf w$就会变得越小,相当于大量隐藏单元的影响变小了(隐藏单元依然存在,因为参数不会为0),导致网络或者说是模型变得简单,根据上图的分析,模型变得简单就能一定程度上避免过拟合,由上图的右图转换为中间图片的情况,即为我们想要得到的情况。
其中,欠拟合和过拟合的状态是相对的,在欠拟合时,我们可以通过增加模型复杂度的方法使模型更能模拟我们想要的函数,但是如果模型复杂度过高,我们就可以通过L2正则化的方法一定程度上降低模型的复杂度,使之由过拟合状态向中间状态转移~
2. 从激活函数
假设我们使用的函数为tanh函数,函数图像如下:
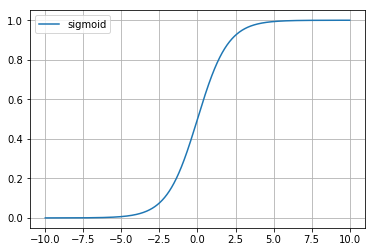
我们可以看到tanh函数在$z$在0附近时,类似于线性的,在非常大或者非常小的时候,类似于非线性的。
因为当我们使用L2正则化时,根据公式2-5所示,会减少了参数的值。进而减少了$z$的绝对值,进而使得激活函数类似于线性函数。
在之前我们讲过(非线性激活函数的必要性),如果激活函数为线性函数,那么神经网络有多少层都是没有意义的,都可以用单层的网络表示,因此可以理解为我们的网络模型变简单了,不会发生过拟合~
4. Dropout(随机失活)
什么是dropout?
之前我们讲过,一个网络过拟合可能因为我们的网络太过于复杂,L2正则化方法就是通过使参数变小,进而使模型变得简单的方法。dropout方法原理类似,只不过它不是减少权值,而是随机的删除某些节点,使得模型的网络结构变得简单,起到正则化的效果。
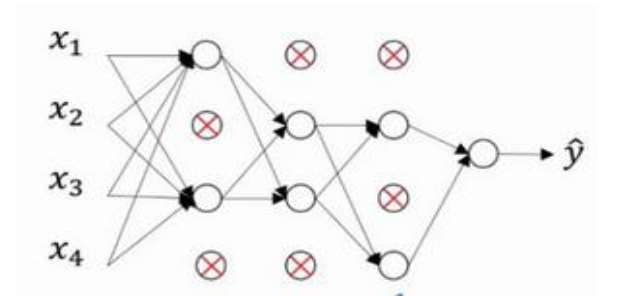
如上图所示,就是随机挑选出一些节点,使其失活,最终使得网络变得简单。
下面介绍一种实现dropout的方法,叫做inverted dropout(反向随机失活):
首先我们生成随机矩阵,然后与keep-prob参数做比较,keep-prob表示保留某个隐藏单元的概率,我们将随机矩阵中小于keep-prob的数字变为1,大于keep-prob的数字变为0,这样,数字为1的概率就为keep-prob。然后我们将转换后的矩阵与激活函数的输出值相乘,这样对应位置为0的隐藏单元就被抹去,不参与计算。
还没有结束,在抹去部分隐藏单元后,我们对保留下来的激活函数的输出值做进一步处理:
\[a/=keep-prop \tag{4-1}\]公式4-1的目的是不影响$a$的期望值(很贴心了~)
注意:我们在测试阶段是不是用dropout方法的,因为在测试阶段进行预测时,我们不期望输出的结果是随机的,如果测试阶段使用dropout方法,预测结果会受到干扰。(采用公式4-1也是为了测试时不采用dropout,激活函数的预期结果也不会发生变化)
5.直观理解dropout正则化
1. 从网络的简易性
dropout的功能使模型变得简单。
在之前的分析中,我们得到结论网络过拟合往往由于网络的复杂性太高,因此随机删除某些节点使得网络更加简单,进而在一定程度上避免过拟合。
2. 与L2正则化对比
加入目前的神经元处于使用dropout正则化的下一层,那么当前的单元不能依赖任何特征,即上一层的输出,因为随时有可能被删除。因此当前单元就不能为某个特征赋予特别大的权重,导致权重收缩,达到类似于L2正则化的效果。
但是也有些许不同:
L2是使得所有的权重都衰减,并且衰减程度不同。
dropout是使得部分隐藏层单元随机消除。
两者相对比,效果上,两者的作用类似,都是减少网络的复杂度,预防过拟合;使用上,Dropout的应用方式更灵活,它可以选择具体在哪几层使用,适用于不同的输入范围。
状态不好写的有点乱~😪
6. L1不可导处理
转载:https://www.zhihu.com/question/38426074/answer/76683857
对于目标函数中包含加性的非平滑项并使用梯度下降求解的问题,如果可以使用proximal operator,则解法如下:
假设目标函数为 $\min_x f(x) + h(x)$其中$f(x)$可导,而$h(x)$不可导。
则每步迭代更新为
\[x^{k+1} = Prox_{h,\eta}(x^k - \eta\triangledown f(x^k))\\ Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + h(y)\tag{6-1}\]如果$h(x) = |x|_1$,也就是题目中要求的L1范数正则化,则对应的
\[Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + \|y\|_1 = \hat{y}\\ \hat{y}_i = \begin{cases} x_i - \eta & \text{if}\ x_i-\eta > 0 \\ x_i + \eta & \text{if}\ x_i+\eta < 0 \\ 0 & \text{otherwise} \\ \end{cases}\tag{6-2}\]