1. 什么是梯度消失与梯度爆炸
训练深度神经网络时,所面临的一个问题就是梯度消失与梯度爆炸,它指的是在训练时,导数或者梯度变得非常大或者非常小,往往以指数级别增大或者减小。
我们通过神经网络中的个例进行分析:
假设我们的神经网络有$l$层,每层有两个隐藏单元,每个隐藏单元中的$b$为0,激活函数为$g(x)=x$,结构如下所示:

所以前向计算$\hat y$的值为: \(\hat y = \textbf W^{[l]}\textbf W^{[l-1]}\ldots \textbf W^{[2]}\textbf W^{[1]}\textbf x\tag{1-1}\) 我们在此基础上假设每个权重矩阵为$\textbf W^{[l]}=\begin {bmatrix} 1.5 & 0 \ 0 & 1.5 \ \end{bmatrix}$,它相当于1.5倍的单位矩阵,当我们将其带入公式1-1中,最后的计算结果为$1.5^{l-1}\textbf x$。
如果这个深度网络很大,那么$\hat y$的值也会非常大,并且呈指数级增长(爆炸式)。
如果我们将上面的矩阵换成$\textbf W^{[l]}=\begin {bmatrix} 0.5 & 0 \ 0 & 0.5 \ \end{bmatrix}$,相当于0.5倍的单位矩阵,同样将其带入公式1-1中,最后的计算结果为$0.5^{l-1}\textbf x$,当网络很深时,激活函数的值将以指数级下降,即”消失”。
上述内容是简单讨论一个神经网络及其激活函数的值,实际上它也适用于与层数L相关的导数或者梯度,即梯度也是呈指数级上升或者下降的。
当梯度消失或者爆炸时,训练难度上升,特别是梯度消失时,会导致梯度下降算法的步长特别小,梯度下降算法需要更多的时间进行学习。
2. 权重初始化(Xavier)
第一小节介绍了梯度消失与梯度爆炸,那么有没有方法彻底解决呢?实际上没有(由深度学习的特性引起的,深度学习往往通过网络的深层嵌套拟合复杂的函数)。
但是有一个不完整的解决方案,即更严谨的选择随机初始化参数。
我们仍旧按照第一小节的方法,先以一个神经元为研究对象,再推广到神经网络。
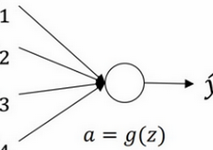
上述神经元计算公式为: \(z=w_1x_1+w_2x_2+\ldots+w_nx_n \tag{2-1}\\ a=g(z)\) 我们同样将$b$忽略不计,为了预防激活函数值的大小,需要通过预防$z$的值的大小。$n$越大时,我们希望$w$越小,因为$z$是$w_ix_i$的和,因此比较合理的方法就是设置$w_i=\frac{1}{n}$,n表示神经元的输入特征的数量。
用python语句表示为$𝑤^{[l]}$=𝑛𝑝.𝑟𝑎𝑛𝑑𝑜𝑚.𝑟𝑎𝑛𝑑𝑛(shape)∗np.sqrt($\frac{1}{n^{l-1}}$),若激活函数为relu时,方差设置为$\frac{2}{n}$会更好,即$w^{[l]}\(=𝑛𝑝.𝑟𝑎𝑛𝑑𝑜𝑚.𝑟𝑎𝑛𝑑𝑛(shape)∗np.sqrt(\)frac{2}{n^{l-1}}$)。
我们分析一下,将权重设置为上述形式,可以使得$z$更趋向于1,这样梯度消失或者爆炸就没有那么快。
3. 梯度检验(grad check)
当我们手动实现BP过程时,无法确定自己写的方程式是否正确,特别是在神经网络比较复杂和向量化的情况下。但是现在有一种方法,它可以检验我们写的BP方程式是否正确,这种方法就是梯度检验。
导数的官方定义: \(f^{\prime}(\theta)=\frac{f(\theta+\epsilon)-f(\theta-\epsilon)}{2\epsilon} \tag{3-1}\) 根据导数的定义我们知道,在$\epsilon$无穷小的时候,就是求解的导数,按照公式3-1的原理,我们事先梯度检验。
首先根据公式3-1做成本函数关于所有参数的导数的近似值: \(d\theta_{approx}[i]=\frac{J(\theta_1,\theta_2,\ldots,\theta_i+\epsilon)-J(\theta_1,\theta_2,\ldots,\theta_i-\epsilon)}{2\epsilon}\tag{3-2}\)
公式3-2中,$\theta$包括正向计算时所有参数,上式就是根据导数的定义计算成本函数关于所有参数的导数的近似值。
在求解$d\theta_{approx}$之后,需要与我们程序中计算的$d\theta$相对比,如果差距不差,说明我们的BP过程是正确的。
检查方法如下: \(\frac{\|d\theta_{approx}-d\theta\|_2}{\|d\theta_{approx}\|_2+\|d\theta\|_2}\tag{3-3}\) 公式3-3的分子就是求解$d\theta_{approx}-d\theta$的欧几里得范数,得到欧氏距离;分母是为了防止分子太大或者太小,使结果成为比率。
其中$\epsilon$一般为$10^{-7}$,如果这个值比$10^{-3}$大很多,那就代表很可能程序有问题,需要进行检测。
当最终结果变成$10^{-7}$是,那就说明程序是没问题的了。
注意事项:
-
仅在调试阶段使用,不能在训练过程中使用,因为计算它比较慢
-
如果算法的梯度检验失败,要检查所有项
-
如果使用正则化,不要忘记在计算时加上正则化