马尔科夫决策过程是形式化序列决策任务的经典工具。
MDP涉及到不同情景下的决策,因此不再是简单的对$q_\ast(a)$ (强化学习基础简介)进行估计,而是对$q_{*}(s,a)$进行估计。
而且当前的行为不仅影响当前的立即回报,还会影响后续的状态,进而影响未来的回报,因此我们需要考虑这种延迟回报问题,权衡立即回报和延迟回报。
有限MDP为拥有有限状态集、有限动作集以及有限回报集的MDP。
1. 智能体-环境
MDP想成为“从与环境的交互接口中学习来达成目标”这一问题最直接的框架。
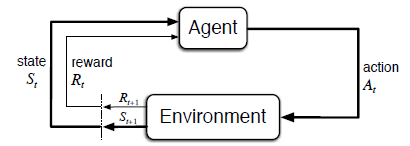
下面来介绍MDP框架的基本要素:
智能体(agent):学习者或者决策者
环境(environment):所有智能体以外的东西叫做环境。具体包括交互的对象以及智能体的某些状态和组成部分。
行为(action):智能体通过行为主观改变环境
回报(reward):环境根据动作发生状态的切换,并且反馈给智能体一个回报信号
状态(state):某种对于环境的表征形式,如特征向量、图片等
轨迹(trajectory):将智能体与环境的交互过程记录下来,就形成了轨迹,格式为:$S_0,A_0,R_1,S_1,A_1,R_2,S_2,\ldots$
转移概率:智能体在某个状态$s$采取某个动作$a$,获得回报$r$并进入状态$s’$,表示为:$p(s’,r \mid s,a) \doteq Pr {S_t = s’, R_t=r \mid S_{t-1} = s, A_{t-1} = a }$,往往又称这个概率分布为MDP的动力学或模型,本质上是环境模型的概率分布(后面涉及到是否已知环境模型就是指这个转移概率)
马尔科夫性:指转移概率$p(s’,r \mid s,a)$完全只和前一个状态有关,不需要考虑前面的决策过程。
怎样区分智能体和环境呢?
任何智能体不能任意改变的东西都被认为是智能体之外的,即环境的一部分。
所以在实际中,我们要区分真正的智能体是什么,往往真正的智能体比我们想的要更细化。
2. 目标和回报
对于智能体来说,我们需要给它一个目标,把目标量化就是我们的回报,实际目标就是:最大化一个长期时间内的累计回报
基于回报的目标表达是十分强大的,例如下棋,目标就是赢,只需要把赢的回报设置为1,其它设置为0,那么智能体就能很好的学习策略了。
某些人可能误以为越复杂的系统,需要设计的回报越精细,其实不是这样的。我们设置目标的本质目的是告诉智能体要什么,而不是告诉他怎么做,这样智能体才能学习到我们意料之外的东西。
下面我们来看如何定义累计回报:
假设在t时刻之后得到的回报序列:$R_{t+1},R_{t+2},R_{t+3},\ldots$
我们用$G_t$表示期望的累计回报,其表达形式为:
\[G_t \doteq R_{t+1}+R_{t+2}+ R_{t+3}+ \dots + R_T \tag{2-1}\]在公式2-1中,我们有终止步长$T$,说明我们的任务不是一直进行的,而是由一个中止状态,这种任务叫做片段式任务(episode tasks);相对应的是连续任务,例如机器人控制。
我们把不包含中止状态的状态集合表示为$S$,加上终止状态的状态集合表示为$S^+$
公式2-1表示的是片段式任务的累计回报;那么连续任务的累计回报怎该怎样表示呢?
不能分割为一个个片段的交互任务叫做连续任务,此时$T=\infty$,如果使用2-1是发散的。为此,我们引入了折扣引子$\gamma$,公式2-1变成:
\[G_t \doteq R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+ \dots + = \sum_{k=0}^\infty \gamma^kR_{t+k+1} \tag{2-2}\]其中$0\leq \gamma < 1$。它的意义是当$\gamma$等于0时,相当于仅考虑立即回报;$\gamma$越大,说明对未来回报考虑的越多,目光越长远。
将公式2-2写成递推的形式:
\[\begin{align} G_t &= R_{t+1} +\gamma R_{t+2} + \gamma^2R_{t+3} + \gamma^3R_{t+4} + \cdots \\ &= R_{t+1} +\gamma (R_{t+2} + \gamma R_{t+3} + \gamma^2 R_{t+4} + \cdots) \\ &= R_{t+1} + \gamma G_{t+1} \end{align} \tag{2-3}\]公式2-3反映了相邻两个状态之间回报的关系。
我们将片段式任务的回报公式和连续任务的回报工时统一,需进行以下假设:
- 定义终止状态为吸收态(absorbing state)
- 进入吸收态的立即回报为0
- 片段式任务的$\gamma$为1

上面假设的目的就是使用与连续任务一模一样的回报形式来定义片段式任务的回报:
\[G_t \doteq \sum_{k=t+1}^T \gamma^{k-t-1}R_k, \quad 0 \leq \gamma \leq 1\tag{2-4}\]这里的T可以取无穷大,关于回报的公式表达一直以公式2-4为代表。
3. 策略和值函数
值函数包括状态值函数和动作值函数,状态值函数用来估计某个状态的期望的未来回报;动作值函数用来估计在某个状态选择某个动作的期望的未来回报。
状态值函数和动作值函数都会基于行为的选择,行为的选择就是指代策略。
策略:一个策略把状态映射到概率分布。随机策略:表示每个可能行为的概率,用$\pi(a \mid s)$表示;确定性策略:每个状态$s$只对应一个动作,即发生概率为1,用$a=\pi(s)$表示。
状态值函数:某个策略$\pi$下选择某个状态$s$的值函数,表示为$v_{\pi}(s)$,定义为从$s$根据$\pi$选择行为能够得到的期望回报。
动作值函数:某个策略$\pi$下的某个状态选择某个动作的值函数,表示为$q_{\pi}(s,a)$,表示为在状态$s$选择行为$a$后,再根据策略$\pi$选择行为能够得到的期望回报。
根据行为值函数我们可以直接得到策略,但是只有状态值函数就不一定能够得到策略了。
下面来看两个值函数的表达式:
- 状态值函数
- 动作值函数
我们说值函数是求解策略的一种手段,但是如何估计值函数呢(在某个策略的基础上)?
我们知道值函数的定义是期望,那么我们可以采集足够的样本,然后进行近似的估计,这就是期望的计算方法。具体我们在策略$\pi$与环境交互的轨迹中,记录每个状态的回报,或者记录每个状态和动作下的回报,然后根据记录求平均值,这样我们就获取了真实的状态值函数和动作值函数,我们把这种方法叫做蒙特卡洛法
当状态空间特别大的时候,通过记录求均值的方式就不现实了,替代的方法是找到一个参数化的函数,通过更新参数使得函数拟合精确的值函数,这种方法叫做值函数近似法
值函数还有一个特性,他们满足一个迭代关系,类似于公式2-3,即当前状态$s$的值函数和下一个状态$s’$的值函数满足:
\[\begin{align} v_\pi(s) & \doteq \mathbb{E}_\pi[G_t | S_t =s] = \mathbb{E}_\pi[R_{t+1} + \gamma G_{t+1} | S_t =s] \\ &= \sum_a \pi(a|s) \sum_{s',r} p(s',r | s,a) \left[ r + \gamma \mathbb{E}_\pi [G_{t+1} | |S_{t+1} = s'] \right] \\ &= \sum_a \pi(a|s) \sum_{s',r} p(s',r | s,a) \left[ r + \gamma v_\pi (s') \right] \tag{3-3} \end{align}\]公式3-3叫做贝尔曼方程,表达了相邻两个状态之间值函数的关系
下面看一下动作值函数的贝尔曼方程:
\(q_{\pi}(s, a)=\sum_{r, s^{\prime}} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma \sum_{a^{\prime}} \pi\left(a^{\prime} | s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right)\right] \tag{3-4}\) 理解状态值函数和动作值函数的贝尔曼方程要从期望入手,我们可以通过备份(回溯)图更好的理解:
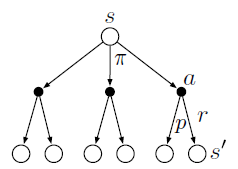
上图为备份图,空点表示状态,实心表示动作,我们可以看到其中一个分支的概率是$\pi * p$,对应的回报为$r+\gamma v(s’)$。那么期望就是对其求和$\sum\sum$。
4. 最优策略和最优值函数
什么是最优策略?在了解最优策略之前,我们先了解什么是“优”,即怎样判断一个策略的好坏。
$\pi \geq \pi’$ 当且仅当对于所有的状态$s\in S$,满足$v_{\pi} \geq v_{\pi’}{s}$
即在所有状态下,一个策略的值函数比另一个策略的值函数都要好,那么说这个策略优于另一个策略,最优顾名思义比所有其他状态都要好。
对于优先MDP问题,实际上存在最优策略,当然最优策略有可能不止一个,但是他们肯定具有相同的状态值函数,我们称最优策略的状态值函数为最优状态值函数,表示为$v_$,最优策略表示为$\pi_$
\[v_*(s) \doteq \max_\pi v_\pi(s) \qquad \textrm{for all}\quad s \in \mathcal{S} \tag{4-1}\]同时,最优策略具有相同的动作值函数,即最优动作值函数:
\[q_*(s,a) \doteq \max_\pi q_\pi(s,a) \qquad \textrm{for all}\quad s \in \mathcal{S}, a \in \mathcal{A}(s) \tag{4-2}\]最优值函数也是值函数的一种,因此他也满足贝尔曼方程,但是最优值函数不依赖于具体的策略。直觉上最优值函数应该是最优策略下最优动作的期望回报(个人认为最优动作将最优策略转换为确定性策略,即概率为1)。表示为:
\[\begin{align} v_*(s)&=\max_{a\in \cal A(s)}q_{\pi_*}(s,a)\\ &=\max_a \Bbb E[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a]\\ &=\max_a \sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')] \end{align}\tag{4-3}\]公式4-3中带入了$q_*(s,a)$的定义,然后对第一个R进行展开。上式叫做状态值函数的贝尔曼最优方程。
同理,动作值函数对应的贝尔曼最优方程为:
\[\begin{align} q_*(s,a)& = \mathbb{E} \left[ R_{t+1} + \gamma \max_{a'} q_*(S_{t+1}, a') | S_t =s, A_t =a) \right] \\ & = \sum_{s', r} p(s',r|s,a) \left[r + \gamma \max_{a'} q_*(s', a') \right] \tag{4-4} \end{align}\]公式4-4同样使用“最优值函数应该是最优策略下最优动作的期望回报”这个直觉。
通过公式4-3和公式4-4可以看出,最优贝尔曼方程和贝尔曼方程的差别在于多了最大化操作。
公式4-3和公式4-4对应的备份图为:
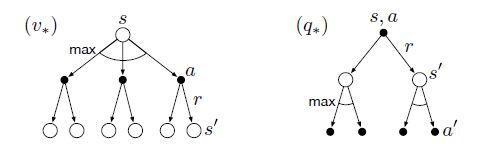
通过备份图可知,在选择动作时,我们并没有根据策略来选择动作,而是使用最大化操作,所以最优贝尔曼方程没有直接和$\pi_*$发生关系。
对于公式4-3而言,有限MDP问题具有唯一解。因此,我们可以根据贝尔曼最优方程求解最优状态值函数或者最优动作值函数。
显示求解贝尔曼最优方程:根据贝尔曼最优方程列出所有状态的非线性方程,然后通过非线性方程求解器求解所有非线性方程的解,即每个状态的值函数(动作值函数同理)。
但是这种方法很少能直接派上用场,它类似于穷举搜索,需要考虑所有的可能性,并且他至少需要三个假设:
- 准确的知道环境模型
- 需要足够的计算资源(毕竟类似于穷举)
- 满足马尔科夫性
因此显示求解贝尔曼最优方程往往行不通。
但是我们通常用近似求解的方法替代显示求解,许多强化学习方法都是在近似求解贝尔曼最优方程(动态规划方法、启发式评估等)
加入求解了最优值函数,如何转换为最优策略呢?
最优值函数分为最优状态值函数与最优动作值函数,我们分别进行分析:
-
最优状态值函数
为了求解最优策略,需要做一步搜索。
在状态s下,搜索所有的$a\in \cal A(s)$,计算$\sum_{s’,r}p(s’,r\mid a,s)[r+\gamma v_*(s’)]$
即$\arg\max_a \sum_{s’,r}p(s’,r \mid a,s)[r+\gamma v_*(s’)]$。
-
最优动作值函数
已知动作值函数更为简单,只需要求$q_\ast(s,a)$最大值对应的动作就是最优行为了。
即$\pi_\ast(s) =\underset{a \in \mathcal{A}(s) } {\arg \max} q_\ast(s,a)$,此时我们可以不清楚环境模型,但是要计算所有的动作值函数。
5. 最优和近似
在第4小节,定义了最优值函数和最优策略,按照之前的方法求解贝尔曼方程即可求得最优策略,但是很难实现,主要受到两方面阻碍:
-
计算能力约束
当状态空间很大时,就会有很多的非线性方程,对这些非线性方程进行求解需要很大的计算资源。在西洋棋例子中,需要上千年才能求解出贝尔曼方程组
-
内存约束
为了建立对值函数、策略以及模型的估计,通常需要大量的内存。对于状态空间不大、有限的任务,可以通过数组或者表格记录所有值函数的值,我们称其为表格式任务,相应的方法为表格式方法。但是实际情况下,状态空间太大,我们必须使用近似的方法,节省内存的使用。
6. 结论
上述内容主要介绍了MDP框架的相关知识,可以看做是强化学习的相关概念与数学模型。
特别是其中的值函数和策略的关系,我们要清楚强化学习最终的目的是学习一个策略,值函数是学习策略的一种手段,当然也有其他手段,但是现阶段我们主要以值函数为主。
以上知识或许在强化学习paper中并没有提及到,但是都是非常基础的,想要更加深入的了解强化学习,MDP框架是必须了解的。
上述内容主要参考《Reinforcement Learning An Introduction》一书。