在之前的学习中,我们学习了MC方法和TD方法,其中TD方法严格说属于TD(0)方法。
如果我们从采样回报与估计回报的角度来看,MC方法与TD(0)方法分别处于两个极端。MC方法采样全部的回报,不使用自身值函数的预测;TD(0)方法只进行单步采样,然后使用值函数预测之后的回报。最好的方法就是这两种的结合,TD(0)属于单步自举,自举最好发生在一段时间之后,$n$-步的方法就是我们在多步之后实现自举。
$n$-步自举和资格迹有很大的关联,一般使用n-步自举作为资格迹的入门介绍。
我们仍然按照广义策略迭代的步骤来分析,先解决预测问题,再解决控制问题。
1. $n$-step TD预测
我们首先来分析一下MC与TD方法之间,存在着怎样一类算法。MC方法的更新依赖从当前状态之后直到终止状态的所有观测,需要仿真完一条完整的轨迹才能进行更新;TD(0)方法仅观测一步$R_{t+1}$,然后就使用下一个状态的估计值来替代之后的累计回报。在MC与TD(0)方法之间,我们可以使用2步、3步…多步来进行观测,再使用之后的状态估计值替代之后的累计回报。
这就是$n$-step TD的思想,看一下示意图:

上图中,最左侧的就是TD(0)方法,最右侧就是MC方法,中间的许多种就是$n$-step TD方法,其意义为我们在当前状态之后,采样了$n$个后续的$R$,然后再使用自举。TD(0)仅采样一个$R$,所有TD(0)也被成为one-step TD方法。
理解了$n$-step TD的思想,我们来分析一下更新目标。
对于一条轨迹$S_t, R_{t+1}, S_{t+1}, R_{t+1}, \dots, R_T, S_T$,MC方法的更新目标为:
\[G_t \doteq R_{t+1} +\gamma R_{t+2} + \gamma^2 R_{t+3} + \dots + \gamma^{T-t-1}R_T \tag{1-1}\]TD(0)的更新目标为:
\[G_{t:t+1} \doteq R_{t+1} + \gamma V_t(S_{t+1}) \tag{1-2}\]相比于MC方法,TD(0)使用$\gamma V_t(S_{t+1})$代表实际的采样$\gamma R_{t+2} + \gamma^2 R_{t+3} + \dots + \gamma^{T-t-1}R_T$,因此,进行递推,2-step TD方法就是采样2步回报:
\[G_{t:t+2} \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 V_{t+1}(S_{t+2}) \tag{1-3}\]再继续扩展到$n$步,更新为:
\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma^n V_{t+n-1}(S_{t+n}) \tag{1-4}\]如果$t+n > T$,那么相当于完全采样,与MC方法等价。
如果使用$n$-step TD方法,有一个必要的条件就是能够观测到$R_{t+n}$才可以,这与MC方法在一个episode之后更新的原理是一样的。我们看一下n-step TD方法的更新公式为:
\[V_{t+n}(S_t) \doteq V_{t+n-1}(S_t) + \alpha [ G_{t:t+n} - V_{t+n-1} (S_t)], 0 \leq t \lt T \tag{1-5}\]在获取1-5中值函数的更新公式,我们看一下$n$-step TD的预测代码:

伪代码中核心公式就是公式1-5的更新,但是一个比较绕的地方就是时间步的确定与计算。
使用n-step TD后,我们来看一下其重要的性质:
\[\max _{s}\left|\mathbb{E}_{\pi}\left[G_{t : t+n} | S_{t}=s\right]-v_{\pi}(s)\right| \leq \gamma^{n} \max _{s}\left|V_{t+n-1}(s)-v_{\pi}(s)\right| \tag{1-6}\]公式1-6中,$v_{\pi}(s)$是状态$s$的真实值,说明在最坏的情况下,使用$n$-step回报得到的估计误差是原始误差的$\gamma ^n$倍,这就是误差缩减特性。
通过实际使用中,MC、TD(0)、$n$-step TD方法的对比,证明在$n$取中间值时,误差最小,这说明MC与TD(0)处在两个极端,比较合适的还是n-step TD方法。
2. n-step Sarsa
我们回顾一下在Sarsa算法中,值函数的更新公式:
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ {R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})} -Q(S_t, A_t)) \right] \tag{2-1}\]Sarsa的更新按照TD(0)的方式进行,我们将更新目标换成n-step TD估计,就是n-step Sarsa算法。
我们列出n-step TD的更新目标的动作值函数版本:
\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma^n Q_{t+n-1}(S_{t+n}, A_{t+n}) , \quad n \ge 1 , 0 \le t \lt T-n\tag{2-2}\]公式2-2与公式1-4几乎完全一样,我们使用公式2-2的更新目标替换公式2-1中的更新目标:
\[Q_{t+n}(S_t, A_t) \leftarrow Q_{t+n-1}(S_t, A_t) + \alpha \left[ {G_{t:t+n}} -Q_{t+n-1}(S_t, A_t) \right] \tag{2-3}\]公式2-3就是n-step Sarsa算法的核心。
我们看一下其伪代码(预测):

自然地,之前还提到过Sarsa的其他版本,如期望Sarsa,按照Sarsa的扩展方法,我们同样可以把期望Sarsa扩展到n-step 期望Sarsa:
\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma^n \bar{V}_{t+n-1}(S_{t+n}) , \quad n \ge 1 , 0 \le t \lt T-n\tag{2-4}\]| 公式2-4中,$\bar{V}t(s) = \mathbb{E}\pi [Q_t(s, a)] = \sum_a \pi(a | s) Q_t(s,a)$,求取期望的步骤仍然在。 |
经过上述两种算法的学习,我们看一下相关备份图:
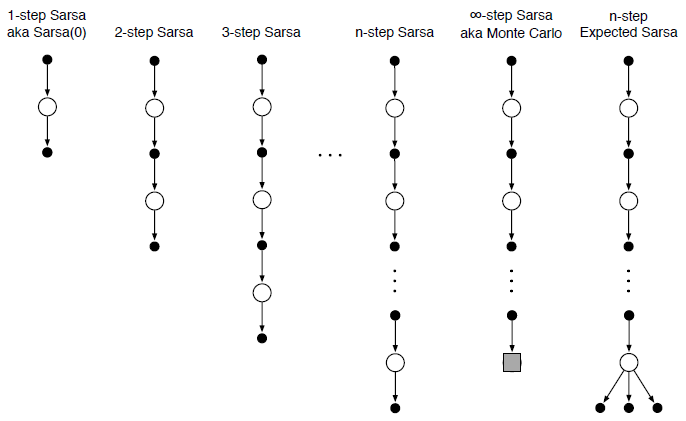
3. n-step off-policy
第2小节我们把n-step的思想使用在Sarsa上,即一个在策略上面,如果现在的算法是off-policy,我们有没有可能使用呢?
我们先来分析一下,off-policy涉及到两个策略,一个是目标策略,也就是我们需要优化的策略;还有一个是行为策略,指的是实际进行决策产生轨迹的策略。一般是利用行为策略产生的轨迹进行目标策略的学习,既然是使用其它策略的轨迹学习,在之前的学习中,就涉及到重要性采样比的问题,因此,在off-policy上使用n-step,难点也是重要性采样比。
使用重要性采样比之后的,策略更新公式为:
\[V_{t+n}(S_t) \doteq V_{t+n-1} (S_t) + \alpha \rho_{t:t+n-1} \left[ G_{t:t+n} - V_{t+n-1}(S_t) \right], 0 \le t \lt T \tag{3-1}\]公式3-1中,相比于Sarsa增加的是重要性采样比$\rho$,其定义为:
\[\rho_{t:h} \doteq \prod_{k=t}^{\min (h, T-1)} \frac{\pi(A_k|S_k)}{b(A_k|S_k)} \tag{3-2}\]公式3-2相当于计算采样的轨迹中,每个动作的采样比,然后进行相乘。
当$\pi$与$b$完全一样时,就退化成on-policy的形式,说明on-policy只是off-policy的一种形式,我们将公式3-1进行改造,得到off-policy下的n-step Sarsa算法:
\[Q_{t+n}(S_t, A_t) \doteq Q_{t+n-1} (S_t, A_t) + \alpha {\rho_{t+1:t+n} }\left[ G_{t:t+n} - Q_{t+n-1}(S_t, A_t) \right], 0 \le t \lt T \tag{3-3}\]相比于公式3-1,状态值函数变为动作值函数,原因是在不知道环境模型的情况下,我们没办法通过状态值函数获取到策略,相反,动作值函数却可以。
得到了off-policy下的n-step Sarsa算法的核心更新公式,我们看一下:

4. n-step备份树算法(off-policy):无重要性采样
通过标题可知n-step备份树算法属于off-policy,但是却不使用重要性采样,到目前为止,我们所有的off-policy算法都使用重要性采样来作为行为策略到目标策略的桥梁,但是备份树由于特殊的备份操作,并不需要,我们来具体看一下:
备份树算法的主要思想:
- 树结构
- 在树结构上执行备份操作:通过后续状态的值更新当前状态的值,叫做备份
我们首先看一下3-step 备份树算法的备份图:
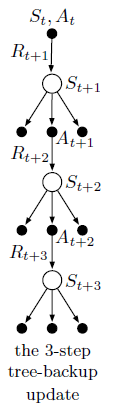
通过备份图我们可以看到,在每一个状态中,算法没有仅取当前选择的动作,而是将所有可能的动作都列出,然后从选择的动作再向下延伸。备份图中有采样的节点,也包括没有采样到的节点,最终构成树结构。
备份到底是怎样定义的呢,我们来看一下具体公式:
对于第一步的备份算法,即备份图中第一层,更新目标为:
\[G_{t:t+1} = R_{t+1} +\gamma \sum_a \pi(a|S_{t+1})Q_t(S_{t+1}, a) , \qquad t \lt T-1 \tag{4-1}\]公式4-1中,可以看到相当于考虑了所有的动作值。
对于二步备份算法,即第一层+第二层,更新目标为:
\[G_{t:t+2} = R_{t+1} +\gamma \sum_{a \neq A_{t+1}} \pi (a|S_{t+1})Q_{t+1} (S_{t+1}, a) \\ +\gamma \pi(A_{t+1}|S_{t+1}) \left(R_{t+2} + \gamma \sum_a \pi(a|S_{t+2}) Q_{t+1} (S_{t+2}, a) \right) \\ = R_{t+1} + \gamma \sum_{a \neq A_{t+1}} \pi (a|S_{t+1})Q_{t+1} (S_{t+1}, a) + \gamma \pi(A_{t+1}|S_{t+1}) {G_{t+1:t+2}}\\ \tag{4-2}\]其中,$t \lt T-2$,二步算法与一步算法很类似,相当于权重变为第一步的权重乘以当前的概率。
我们总结出n-step备份树算法的迭代公式为:
\[G_{t:t+n} = R_{t+1} +\gamma \sum_{a \neq A_{t+1}} \pi (a|S_{t+1})Q_{t+n-1} (S_{t+1}, a) + \gamma \pi(A_{t+1}|S_{t+1}) {G_{t+1:t+n}}\tag{4-3}\]其中,$t \lt T-1,n \geq 2$ 。
有了公式4-3,我们可以按照n-step Sarsa的更新算法格式:
\[Q_{t+n} (S_t, A_t) \doteq Q_{t+n-1}(S_t, A_t) + \alpha \left[ G_{t:t+n} - Q_{t+n-1}(S_t, A_t) \right]\tag{4-4}\]作为备份树算法的更新公式。
下面来看伪代码:

在备份树算法中,使用完全随机的决策作为行为策略,肯定是off-policy无疑了。
个人理解,备份树的备份操作实际上和重要性采样的作用是一样的,只不过备份树使用概率的方法来作为重要性采样中的比值。
5. 总结
在上述学习中,一共学习了3种算法:n-step Sarsa算法、off-policy n-step Sarsa算法、n-step 备份树算法,他们实际上都是n-step思想的运用。
n-step处于TD(0)与MC方法思想的中间,相当于结合MC方法与TD(0)方法。有时候部分采样+部分自举的结果往往更好。
上述内容主要参考《Reinforcement Learning An Introduction》一书。