1. 边缘检测
当我们获取到一张图片时,我们想要知道这张图片中有什么物体,为了实现这个目的,我们做的第一件事就是边缘检测,可能需要检测垂直边缘,也可能同时需要水平边缘,但是边缘检测是怎样做的?原理是怎样的呢?
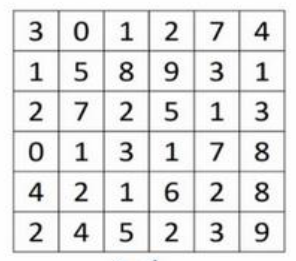
如上图所示,是一张灰度图像,是$6\times 6\times 1$的矩阵,因为是灰度的,所以没有RGB通道,不是$6\times 6\times 3$的。
为了检测上述图像,我们需要构造一个$3 \times 3$的过滤器,过滤器长这个样子:
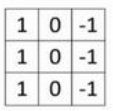
我们使用上述过滤器对突图像进行卷积操作:
首先使用过滤器对图像左上角的$3 \times 3$矩阵做元素乘法,然后求和,作为结果的左上角的值:
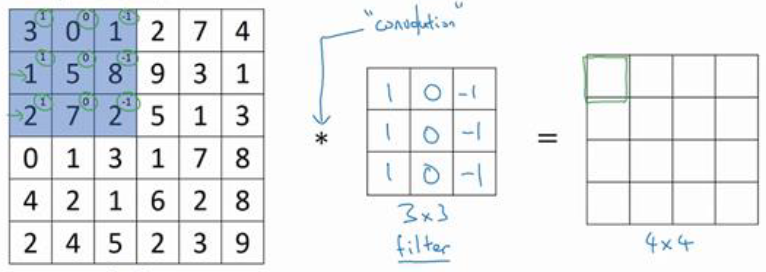
最终求得第一个值为-5。同理,将图像的蓝色区域右移一个单位,继续与过滤器做卷积操作,得到第2个值,放在第二个位置上。
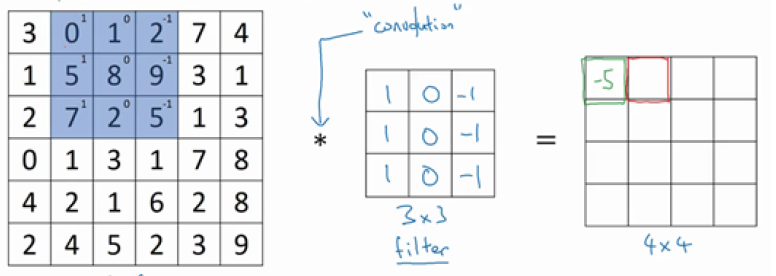
最终不断迭代上述过程,求得$4 \times 4$的矩阵。
我们分析一下上述过程,左面的矩阵是一张图片,中间是过滤器,后面的矩阵也可以理解为一张图片,这就是垂直边缘检测器的原理。
但是为什么上述步骤就能实现垂直边缘检测呢?
我们首先构造一个拥有垂直边缘的图像:
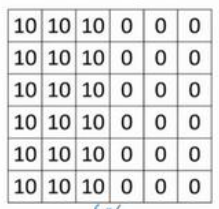
其中左半部分都为10,代表比较亮的像素值;右半部分都为0,代表比较暗的像素值;因此,垂直边缘就在中间。我们仍然使用上述的过滤器对这个图像进行卷积操作:
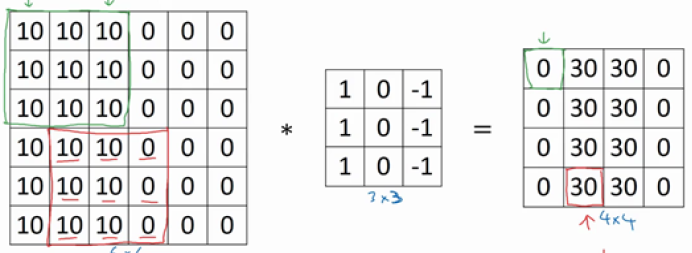
最终求得值为上图所示。其中过滤器的左边为1,代表明亮的像素;中间为0,代表过度;右边为-1,代表较暗的像素。最终得到上图中右边的矩阵,或者称之为图像。其中间为30,左右都为0,代表中间亮两边暗的情况,这不就是我们要求解的垂直边缘吗。
我们使用形象的图示表示上述过程:

通过卷积运算,我们将原始图像的垂直边缘显示出来,当然,这个垂直边缘在最终图像中有点粗,这是由于原始图像矩阵太小导致的,当我们使用$1000 \times 1000$的原始图像时,效果就会好得多。
上面的原始图像是左亮右暗,如果换成左暗右亮会怎样呢,我们来做一下实验:
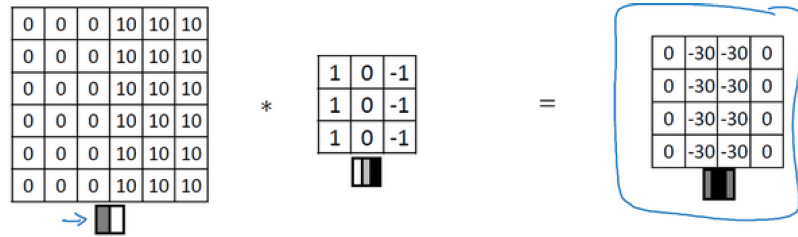
最终也会获得一个垂直边缘检测的图像,只不过垂直边缘是深度的,两边是浅色的。这样,我们通过最终图像的亮暗区别就能得到原始图像的正边和父边,即由亮到暗还是由暗到亮。如果我们不care这个区别,我们在进行卷积操作时,完全可以取最终结果的绝对值。
上面的内容都是垂直边缘检测的内容,如果是水平边缘检测,我们应该使用什么样子的过滤器呢?其实很容易猜到:

上图中左面是垂直边缘检测过滤器;右边是水平边缘检测过滤器。
在计算机视觉的文献中,还讨论过不同的过滤器哪种最好,我们简单介绍几种:
-
Sobel过滤器
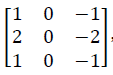
相当于在中间增加了一行元素的权重,使得结果更加鲁棒。
-
Scharr过滤器
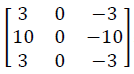
在深度学习中,我们可以不使用上述的几种过滤器,而是将过滤器中的9个数字作为9个参数,然后在图像中使用DP算法去学习这些参数。通过学习,我们可以获取上述的几种过滤器,甚至还会获取更先进的过滤器:不仅能单纯的检测垂直边缘和水平边缘,还能检测$45^\circ$、$70^\circ$、$73^\circ$甚至任何角度的边缘
2. padding(填充)
第一小节通过边缘检测,展示了卷积操作是怎样运算的,下面我们来看一个常用的卷积操作padding。
在第1小节中,我们使用$6\times 6$的原始矩阵,$3 \times 3$的过滤器,得到$4 \times 4$的图像,用数学表示为,原始图像为$n \times n$,过滤器为$f \times f$,最终图像为$(n-f+1)\times (n-f+1)$。
通过分析,我们知道卷积操作会存在两个缺点:
- 图像会缩小,如果不停的做卷积,最终可能得到$1 \times 1$大小的图像
- 原始图像角落边缘的像素,被过滤器使用的概率特别小,但是中间的像素值,被使用的频率很高,这意味着我们丢失了图像边缘位置的信息
为了解决上述问题,我们可以在卷积操作之前填充原始图像。还是以第2小节为例,我们可以在原始图像周围填充一圈0,这样原始图像由$6 \times 6$变为$8 \times 8$,我们带入公式,最终的图像为$(8-3+1)\times (8-3+1)$,为$6 \times 6$,即与原始图像的大小相同。当然,在填充时,一般填充0.
我们使用数学公式描述填充过程,原始图像为$n \times n$,过滤器为$f \times f$,填充数量为p,那么最终图像为$(n + 2p-f+1)\times (n + 2p-f+1)$
在实际工程找那个,填充多少像素一般有两个选择:
-
Valid
不填充,计算公式为$(n-f+1)\times (n-f+1)$
-
Same
填充,且填充后,输出的图像大小和输入的图像大小是一样的。
即$(n+2p-f+1)=n$,求解$p=\frac{f-1}{2}$,可见只有f为奇数,才能得到整数值
为什么在计算机视觉中,$f$通常为奇数呢?
原因如下:
- 如果f是偶数,在使用Same填充方式时,只能使用不对称填充
- 使用奇数的过滤器,会有一个中心点,在计算机视觉中,有一个中心像素点会更方便,便于指出过滤器的位置。
3. Stride(步长)
卷积神经网络的另一个基本操作是步长(stride)
现在我们的原始图像是7 \times 7扥,过滤器是3 \times 3的,假如我们将步长设为2,看一下具体的操作:
第一步:
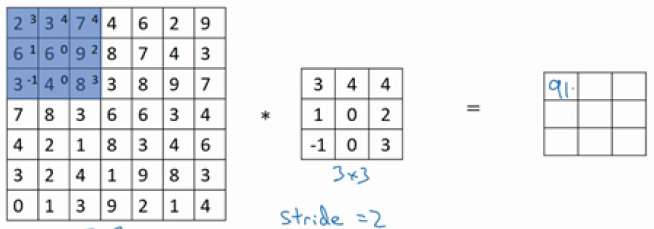
第二步:
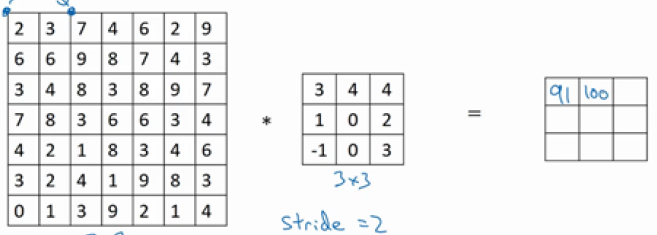
我们可以看到与过滤器进行元素乘法的矩阵直接向右移动了2个单位,这就是步长为2的作用。
我们使用数学公式表示一下,原始图像为$n \times n$,过滤器为$f \times f$,填充数量为p,步长为s,现在我们得到的图像为$(\frac{n+2p-f}{s}+1) \times (\frac{n+2p-f}{s}+1)$。
在上述的例子中,求得最终图像为$3 \times 3$
现在考虑一个问题,当$\frac{n+2p-f}{s}+1$不是整数怎么办?我们应该使用向下取整的操作,意义为当与过滤器进行元素乘法的矩阵移动到外面时,不进行运算,最后修正为$\lfloor \frac{n+2p-f}{s}+1\rfloor \times \lfloor\frac{n+2p-f}{s}+1\rfloor$。
实际上,上述的操作在数学中并不叫做卷积运算,数学中的卷积需要先做镜像操作(研水平和垂直轴翻转),然后再进行上述的操作;我们的上述操作实际上叫做互相关,但是在文献中,把它叫做卷积。
数学中卷积的镜像操作:
翻转前:

翻转后:
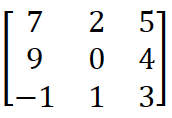
4. 三维卷积
当我们使用的图像不是灰度图像时,我们原始图像应该是$6 \times 6 \times 3$,其中3为RGB彩色特征。现在我们要对这个彩色图像做卷积,使用的也不是$3 \times 3$的网络,而是$3 \times 3 \times 3$ 的过滤器。
在$6 \times 6 \times 3$与$3 \times 3 \times 3$中,第一个数叫做高度、第二个数叫做宽度、第三个数叫做通道数。其中原始图像和过滤器的通道数必须相等。
我们来看一下三维卷积操作:
第一步:
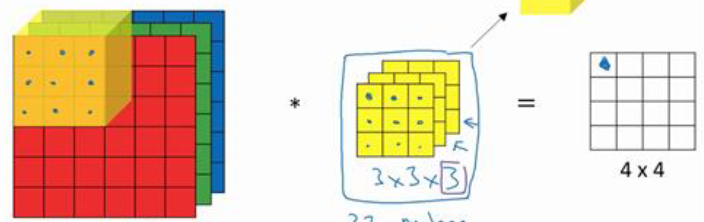
相当于将三维的过滤器与三维的原始图像做元素乘积,然后求和,在上述例子中,相当于过滤器拥有27个参数,进行元素乘积后,也会有27个值,将这27个值求和,即可得结果图像的第一个值。
剩下的15步操作过程与上述过程同理。
假如上述过滤器做的是对RGB三个彩色通道做垂直边缘检测,现在我想要同时检测水平边缘检测怎么办?
现在我们就需要多个过滤器!
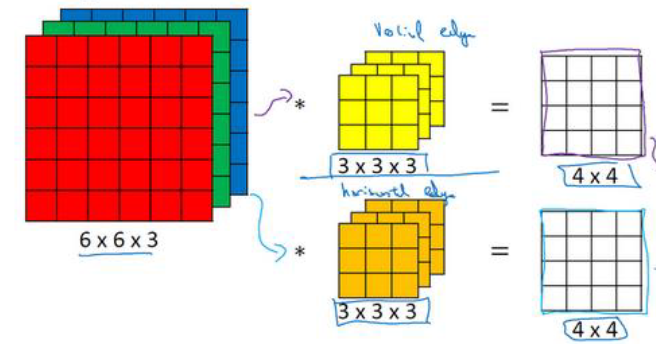
如上图所示,第一个过滤器做的是垂直边缘检测,第二个过滤器做的是水平边缘检测,他们都能得到一个$4 \times 4$的图像,将这两个图像堆叠在一起,就得到了$4 \times 4 \times 2$的输出立方体。
我们使用数学公式表达上述过程,我们的输入为$n \times n \times n_c$,其中$n_c$表示通道数,卷积一个$f \times f \times n_c$的过滤器,这里假设p=0,s=1,得到的图像值为$(n-f+1) \times (n-f+1) \times n_c \times n_c’$,其中$n_c’$表示过滤器的个数,也是下一层输入图像的通道数。
5. 卷积层与池化层
首先看一下什么是卷积层:
在前向传播过程中,我们会进行两个操作$z=wx+b,a=g(z)$,上述的卷积操作相当于$wx$的过程,每个过滤器拥有一个b,然后再对增加b的值使用非线性函数。
我们可以结合普通的网络进行理解,在深度学习中,每个神经元相当于一个过滤器,它是$n \times n \times n_c$的,有多少个过滤器就相当于多少个神经元,每个神经元拥有一个$b$,然后使用python的广播机制对每个z值应用非线性函数。
卷积层实际上就是将卷积操作带入神经网络中的前向传播中。
下面看一下池化层:
池化层通常和卷积层配合使用,用来缩减模型的大小,提高计算速度,同时提高提取特征的鲁棒性。
我们首先莱来看一下最大池化操作:
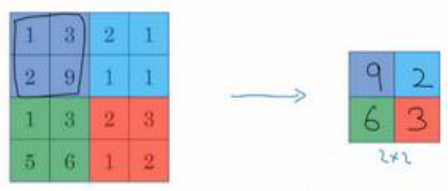
如上图所示,执行最大池化的矩阵是$2 \times 2$的矩阵,$4 \times 4$的矩阵处理后,得到$2 \times 2$的输出。
相当于使用了$2 \times 2$的过滤器,步长为2。
我们对最大池化操作进行一下直观理解,如果在过滤器中提取到某个特征,那么保留其最大值,如果没有提取到这个特征,可能是在象限中不存在这个特征,那么获取的最大值还是很小。
池化的一个特点是,它拥有一组超参数(n与s),但是并不需要进行学习,他是一个固定运算,梯度下降无需改变任何值。
除了最大池化之外,还有平均池化,选取的是每个过滤器的平均值,最大池化比平均池化常用。
池化层知识神经网络某一层的静态属性,不需要进行学习。
一般来说,卷积神经网络一般使用卷积层CONV、池化层POOL与全连接层FC一起使用。
一种常用模式为CONV1+POOL1+CONV2+POOL2+FC1+FC2(一个卷积层与一个池化层配合使用)
另一种为CONV1+CONV2+CONV3+POOL1+CONV4++CONV5+POOL2+FC1+FC2(一个或多个卷积层跟一个池化层)
6. 卷积的优势
通过简单的计算,我们会发现卷积网络相比于全连接网络,参数的数量少的多,这是卷积网络的优势,为什么卷积网络的参数这么少呢?主要考虑一下两个方面原因:
-
参数共享
一个特征检测器(过滤器),目的是垂直边缘检测,能够检测图片左上角区域的特征,也适用于图片的右下角区域,因此在检测左上角区域与右下角区域的特征时,不需要添加其他的特征检测器。
-
稀疏连接
输出像素中的某个单元,仅与输入特征中的少部分相连接(卷积过程),其他像素值不会对当前输出像素的某个单元产生影响,这就是稀疏连接。
全连接网络中,输出的每一个值都是由所有的输入得到的。
7. 经典网络
-
LeNet-5
识别灰度图像的手写数字,由于针对灰度图像设计,因此原图像为$32 \times 32 \times 1$
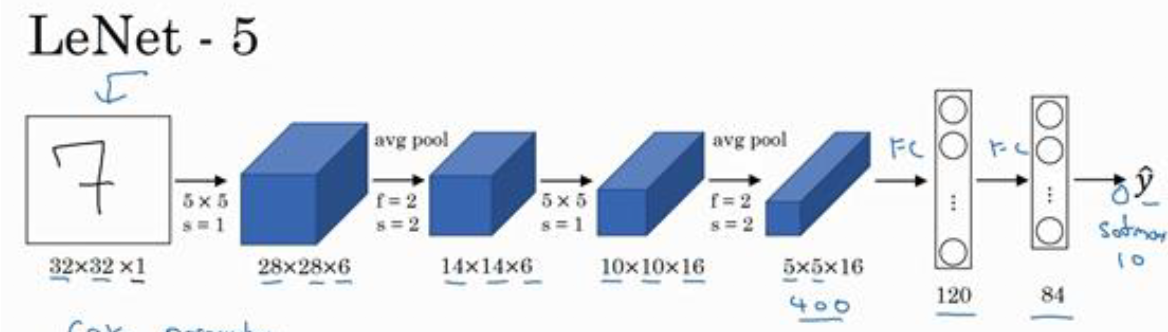
LeNet-5的网络结构如图所示,先使用一个$5 \times 5$的卷积层,得到$28 \times 28$的输出,再使用平均池化,输出为$14 \times 14 \times 6$的输出,然后重复上述两个过程,最终得到$5 \times 5 \times 16$的输出,然后再接两个全连接层,使用softmax得到输出。在网络中,激活函数为sigmoid和tanh。
-
AlexNet
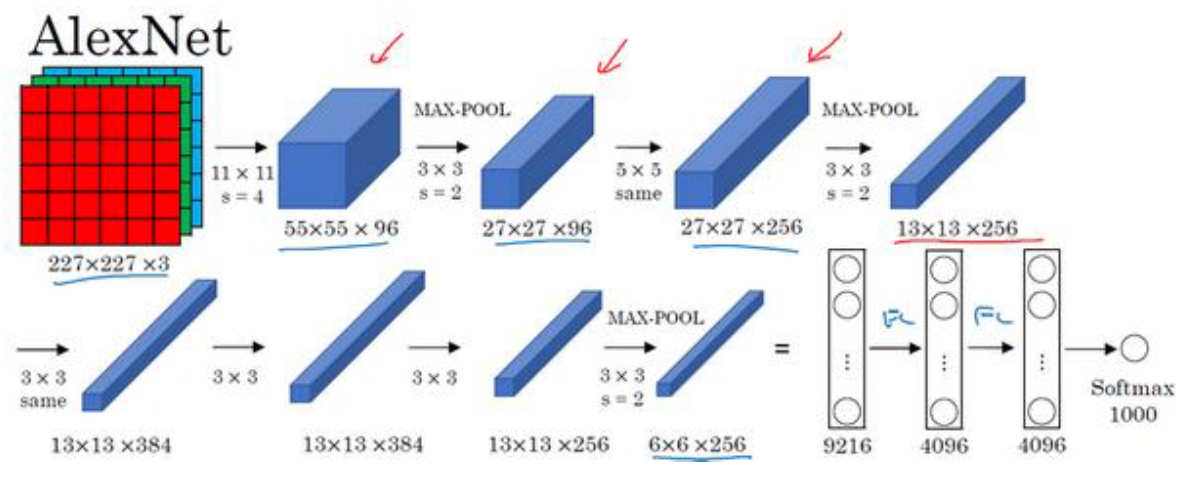
AlexNet相比于LeNet其实差别不大,但是它有更好的效果,原因是使用了更多的隐藏单元和数据,且使用了relu激活函数和最大池化。
通过AlexNet这篇论文,计算机视觉群体开始重视深度学习,并确信深度学习可以用于计算机视觉领域
-
VGGNet
也叫作VGG-16网络,是一种专注构建卷积层的简单网络,他的优点在于简化了神经网络结构。
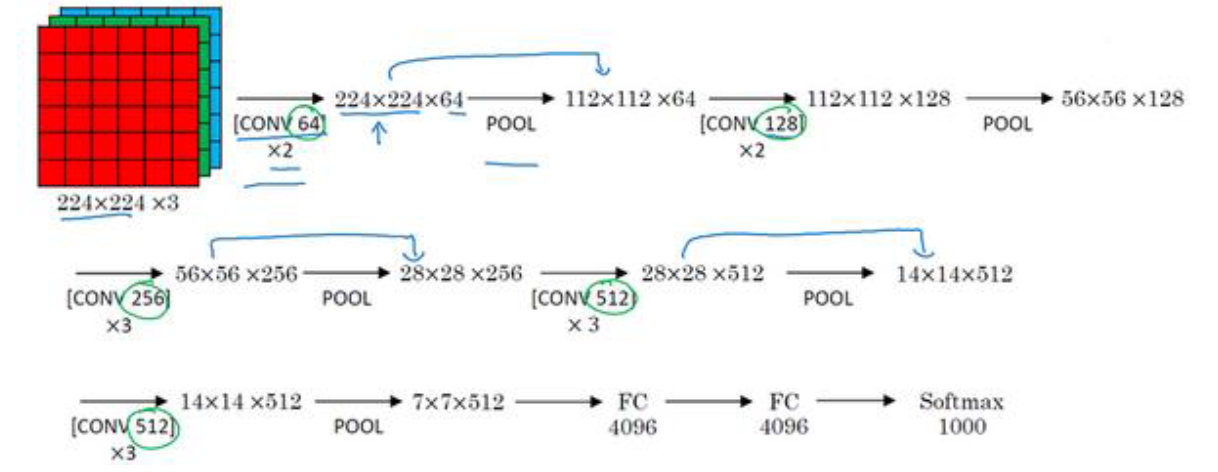
它的结构很规整,卷积层加上FC层一共有16个,在卷积过程中,使用Same填充,我们可以看到卷积层的过滤器数量由64增长为128、256、512。这种相对一致的网络结构很吸引人,但是缺点就是特征数量非常巨大。
8. 残差网络(ResNets)
我们知道非常深的网络时很难训练的,因为存在梯度消失和梯度爆炸的问题。我们可以使用一种技术,叫做跳跃连接(Skip connection),他可以从某一层网络层获取激活值,然后迅速反馈给另外一层,甚至是更深的层,ResNets就是利用跳跃连接构建的。
想要了解残差网络,先来看一下残差块:
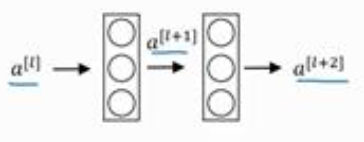
如上图所示,我们截取神经网络中的两层,我们可以认为输入时$a^{[l]}$,经过以下步骤:
\[a^{[l]} \rightarrow z^{[l+1]} \rightarrow a^{[l+1]} \rightarrow z^{[l+2]} \rightarrow a^{[l+2]}\tag{8-1}\]公式8-1的过程就是上述两层网络的计算过程。
残差块是怎样在上述计算过程中运作的呢?
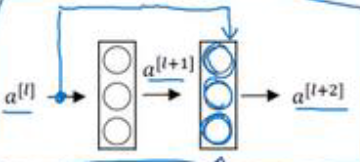
如上图所示,$a^{[l]}$直接向更深网络传递,传递到$z^{[l+2]} \rightarrow a^{[l+2]}$之间,原来$a^{[l+2]}$的计算方式为$a^{[l+2]}=g(z^{[l+2]})$,增加残差块之后,计算方式为$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$,也就是说增加的$a^{[l]}$产生了残差块。
上述$a^{[l]}$直接跑到更深层也可以叫做跳跃连接,意思是跳过好几层,将信息送到更深层的网络。
了解了残差块,我们就可以正是了解ResNets,它的发明者是何恺明(Kaiming He)、张翔宇(Xiangyu Zhang)、任少卿(Shaoqing Ren)和孙剑(Jiangxi Sun),他们发现使用残差块能够训练更深的神经网络。所以构建一个ResNets网络通过将很多这样的残差块堆积在一起,形成一个很深的网络。
我们通过一幅图对比一个深层网络拥有残差块和没有残差块的区别:
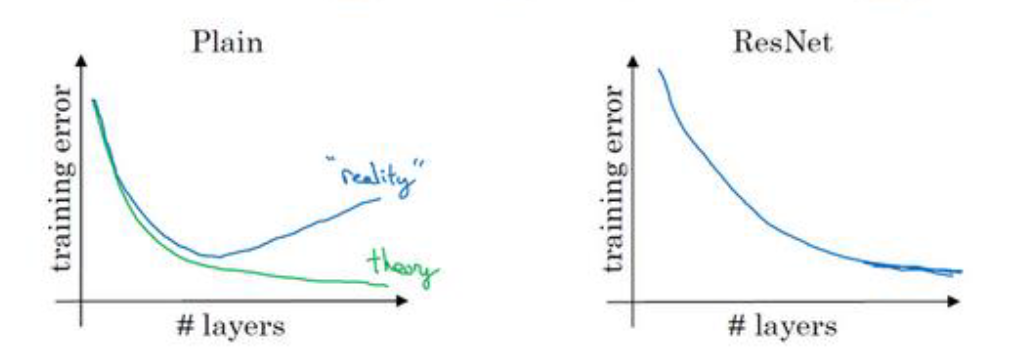
如上图所示,左面的图表示无残差块的网络,理想中网络越深,训练应该越来越好,实际上训练错误会先减少然后增多,因为网络越深使用优化算法越难训练。增加了残差块的网络则避免了这个问题,虽然网络很深,但是使用跳跃连接的手段,使得很深的网络也可以得到很好的训练。
会什么残差网络会生效呢?我们进行一下分析
加入目前我们有一个大型神经网络,输入为X,输出为$a^{[l]}$,现在我们想要增加网络的深度,依次添加两层,最后输出为$a^{[l+2]}$,过程如下图所示:
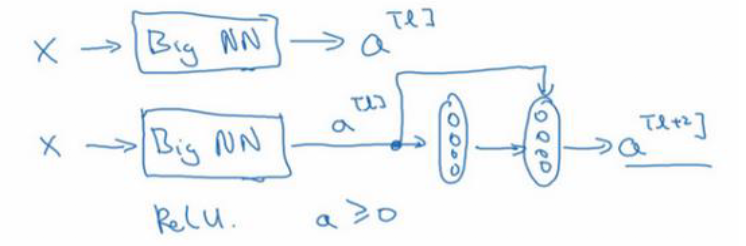
由于我们使用了RELU激活函数,所以所有的激活值都大于等于0,增加两层后,我们得到的$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$,我们对$z^{[l+2]}$进行分析,其一定大于等于0,当权重为0时,它将等于0,即$a^{[l+2]}=a^{[l]}$,相当于恒等式。
这说明什么?说明网络是有可能通过学习参数,将增加的两层变为恒等式,这样就不会逊色于简单的网络(浅层)。
当然,上述分析仅仅是使得保持与浅层网络相同的效率,当我们增加的两层学习到更有意义的信息的时候,他可能比学习恒等式要好,这就说明效率会提升;但是普通的深层网络,即使学习到恒等式都很难。
这就是残差块有效的主要原因。
残差网络还有一个细节是$z$与$a$的维度,我们再使用卷积网络时,尽可能使用Same填充,这样$z+a$不会改变维度,使得残差块的实现很容易,对于一个普通的深层网络,如果使用Same填充,那么可以很轻易的实现残差块。
9. $1 \times 1$卷积
$1 \times 1$卷积听起来没什么用,应为相当于乘以一个数字,但是对于多个通道的输入图像却并非如此。
我们来看一下单个通道和多个通道使用$1 \times 1$卷积的区别:
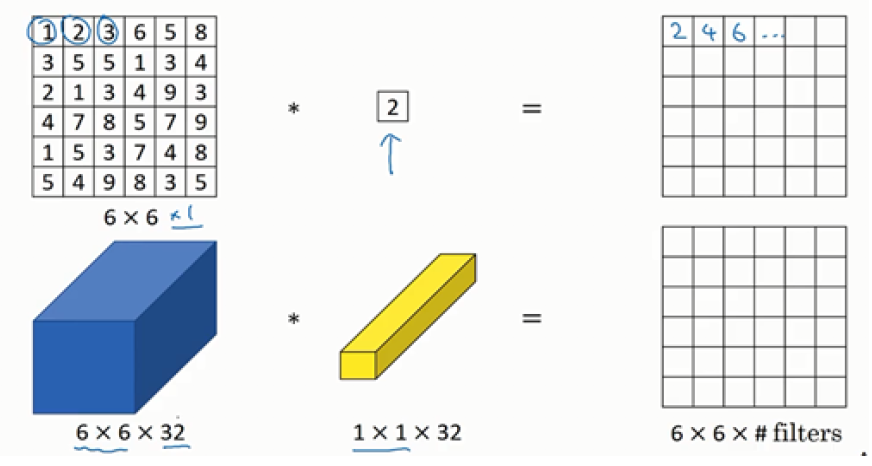
对于单个通道的图像来讲,实际并没有什么用处,但是对于32个通道的输入来说,它相当于对输入的某个通道的32个数字与过滤器做元素乘积,然后求和,并应用relu函数。
这种方法就叫做$1 \times 1$卷积,也被称作Network in Network。
同时,他也可以作为增加或者降低通道数的手段。降低高度和宽度的方法是使用池化层。
10. Inception网络
Inception网络是由Google公司的作者发明的,也被叫做GoogleLenet。
在我们构建卷积层时,我们往往不确定使用$1 \times 1$的过滤器,还是使用$3 \times 3$、$5 \times 5$的,以及是否使用池化层。Inception网络的作用就是代替我们决定这个过程,它会使得网络变得复杂,但是表现却非常好。

如上图所示,分别使用$1 \times 1$、$3 \times 3$、$5 \times 5$以及最大池化层,当然他们的填充方式都是Same的,已保证高、宽一致,不同的只是通道数量。
上图所示的就是Inception模块,它的思想就是不需要人为决定使用哪个过滤器或者是否需要池化层,而是由网络自行确定这些参数,我们可以给网络添加这些参数的所有可能值,然后将这些输出连接,让网络学习它需要什么样的参数,采用哪些过滤组合。
由于我们将所有可能的过滤器都添加到了Inception模块,所以它的运算次数会非常大,此时,我们可以使用$1 \times 1$过滤器,先将通道数减少,然后再使用$3 \times 3$、$5 \times 5$的过滤器,这样会较少运算次数(在一般情况下,$\frac{1}{10}$不是问题)。
通过$1 \times 1$过滤器减少通道数量的层,我们称其为瓶颈层,通过瓶颈层,相当于我们先缩小网络,然后再扩大他。
Inception模块的示意图如下:
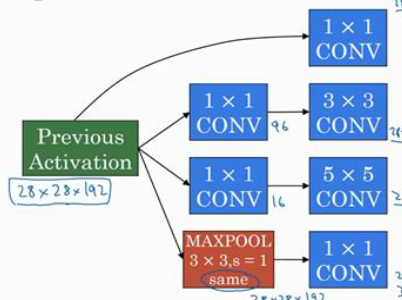
上图所示就是一个完整的Inception模块,我们可以看到$3 \times 3$、$5 \times 5$的过滤器在使用之前,添加了瓶颈层;其中最大池化层因为会保留原有的通道数,我们需要使用$1 \times 1$过滤器减少通道数。
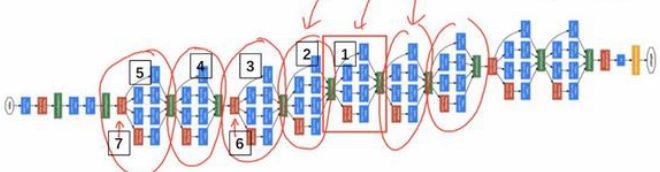
Inception网络就是将上述的Inception模块连接起来,最后接一个FC层,以及softmax层。
计算机视觉数据增强trick:
- 垂直镜像对称(最简单)
- 随机裁剪
- 色彩转换
- 调整RGB通道的值
- PCA(主成分分析):颜色增强