1. 数学建模
我们通过一个例子学习序列模型,这个例子就是命名实体识别,需要能够自动识别语句中人名位置的序列模型。
Harry Potter and Herminoe Granger invented a new spell.
例如上面这个输入,我们的输出应该为:
1 1 0 1 1 0 0 0 0
其中使用$x^{<1>},x^{<2>},x^{<3>},\ldots ,x^{<9>}$表示输入的每个单词,$y^{<1>},y^{<2>},y^{<3>},\ldots ,y^{<9>}$表示输出的每个数字。
$T_x$表示输入序列的长度,$T_y$表示输入序列的长度,在这里$T_x=9,T_y=9$
我们的这个例子是自然语言处理(NLP),我们需要决定怎样表示一个单词:
我们需要先做一个词典,类似于下图所示:
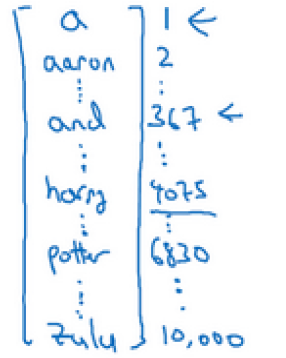
在词典中,每个单词都有一个编号,对于一般商业应用来说30000到50000的词大小的词典比较常见,大型互联网公式可能会用百万大小的词典。
在我们的例子智中,我们选用10000大小的词典。根据上述的词典,我们使用one-hot表示法表示词典中的每个单词。
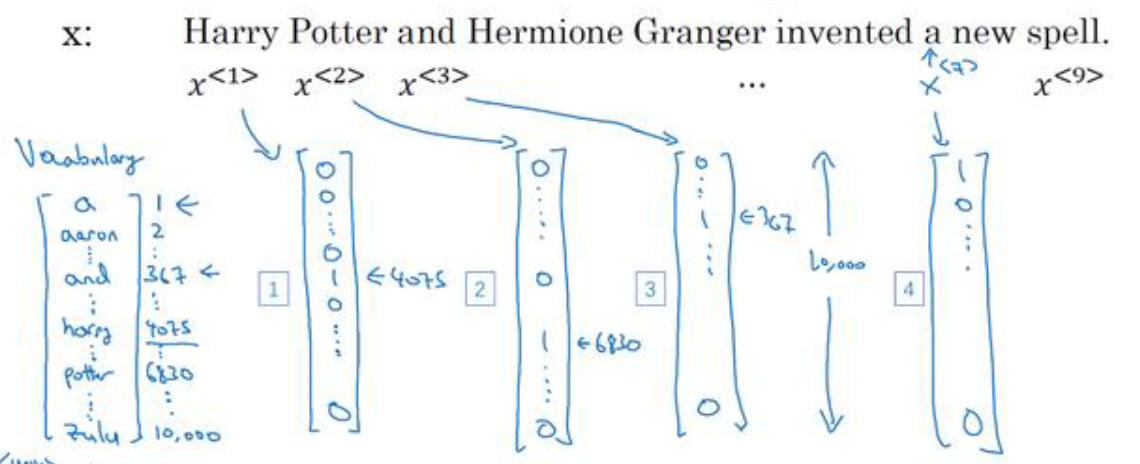
上图所示就是one-hot表示法的具体细节,每个次通过一个10000大小(词典大小)的数组表示,其中单词在词典中的索引位置,将数组中索引位置设为1,这样每个单词所表示的10000大小的数组,仅有一个数字为1。
当我们遇到一个不在字典中的单词,我们需要创建一个新的标记,叫做Unknow Word的伪单词,用<UNK>表示。
2. 循环神经网络(RNN)
通过第1小节,我们明确了例子的输入输出,我们先尝试使用标准网络处理。
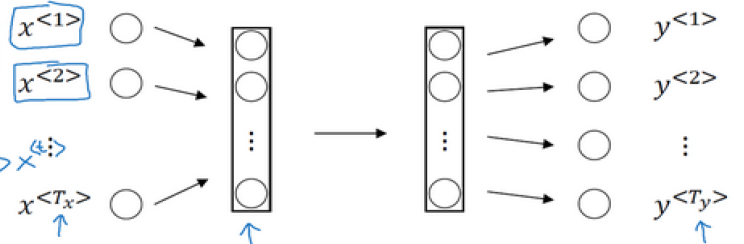
上图就是使用标准网络,即FC网络处理的流程,但是效果并不好,体现在以下两个方面:
- 每个句子的输入输出的长度不一致,即不同语句的$T_x、T_y$不一致,虽然我们可以通过填充(pad)的方式,使每个语句达到最大的长度,但是仍然不是一个好方式。
- 标准的神经网络结构,并不共享从文本不同位置上学到的特征,我们需要共享学习到的信息,类似于卷积网络的权值共享,一个更好的表达方式也会降低参数的数量。
循环神经网络就可以解决上述问题:
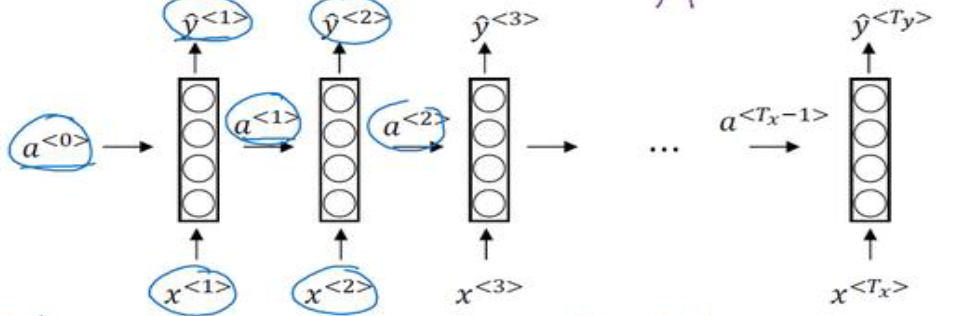
我们来分析一下上述图片,在每一个单词的向量输入网络时,网络不仅使用输入进行预测,同时使用之前网络的处理值。我们来看一下单个词的处理公式:
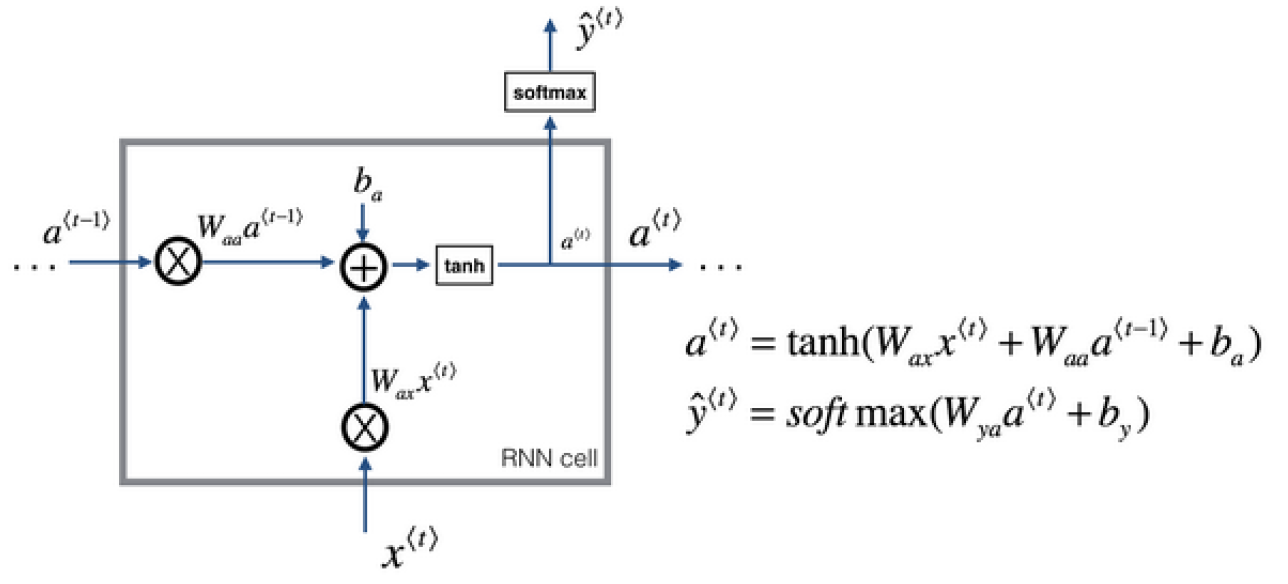
\[a^{<t>}=g_1(W_{aa}a^{t-1}+W_{ax}X^{<t>}+b_a)\\ \hat y^{<t>}=g_2(W_{ya}a^{<t>}+b_y)\tag{2-1}\]如公式2-1所示,在每一个单词的处理过程中,RNN先通过输入$x$与上一个网络的输入$a$计算当前网络的$a$,其中激活函数一般使用tanh,也可以使用relu函数,然后使用当前网络的输出$y$,激活函数可以使sigmoid或者softmax等等。
不停迭代公式所示内容,即为RNN网络的前向传播过程。
我们可以对公式2-1的公式进行简化:
$W_{aa}$与$W_{ax}$可以横向合并成一个向量:$W_a=[W_{aa}\quad fW_{ax}]$
同理,$a^{t-1}$与$X^{
这样,简化后的结果为:
\[a^{<t>}=g_1(W_a[a^{t-1},X^{}]+b_a)\\ \hat y^{<t>}=g_2(W_ya^{<t>}+b_y)\tag{2-2}\]标准RNN前向传播示意图:
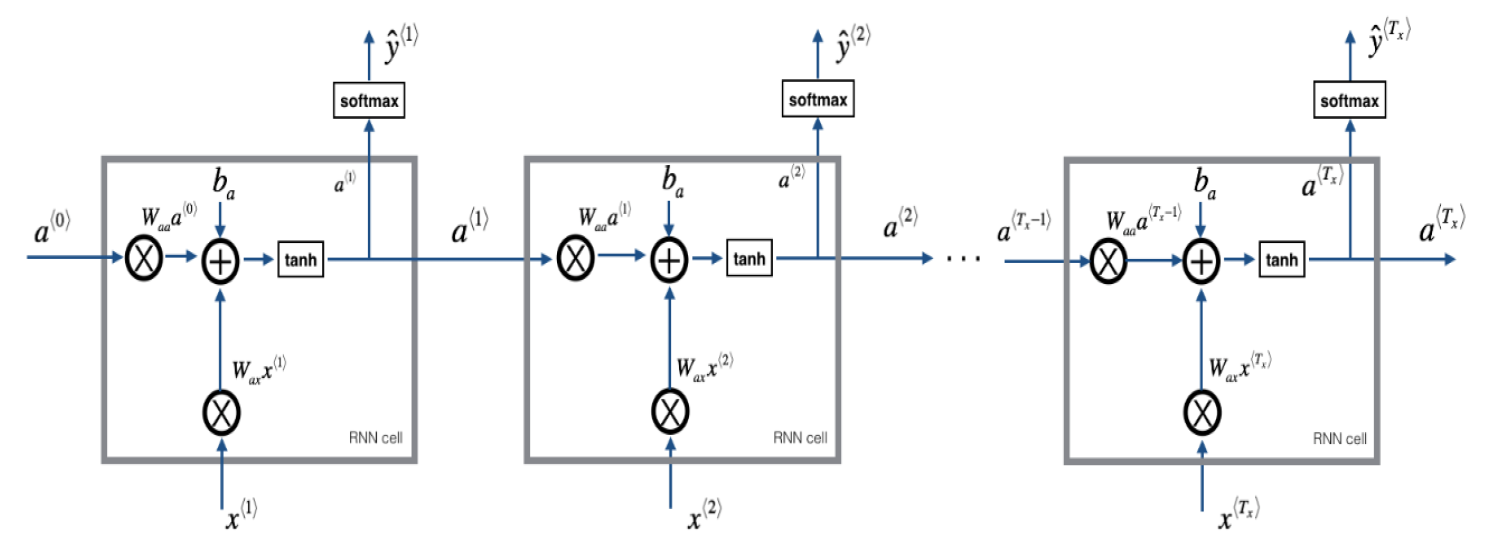
关于RNN的方向传播过程与前向传播相反,我们首先看一下损失函数:
对于一个元素,即单个单词,损失函数如下:
\[L^{<t>}(\hat y^{<t>},y^{<t>})=-y^{<t>}\log \hat y^{<t>}-(1-y^{<t>})\log (1-\hat y^{<t>}) \tag{2-3}\]整个序列的损失韩式为所有元素损失函数的和:
\[L(\hat y,y)=\sum_{t=1}^{T_x}L^{<t>}(\hat y^{<t>},y^{<t>})\tag{2-4}\]反向传播的过程就是前向传播的逆运算,即从右到左的运算,叫做“backprogation through time”。通过时间的反向传播。
反向传播示意图如下:
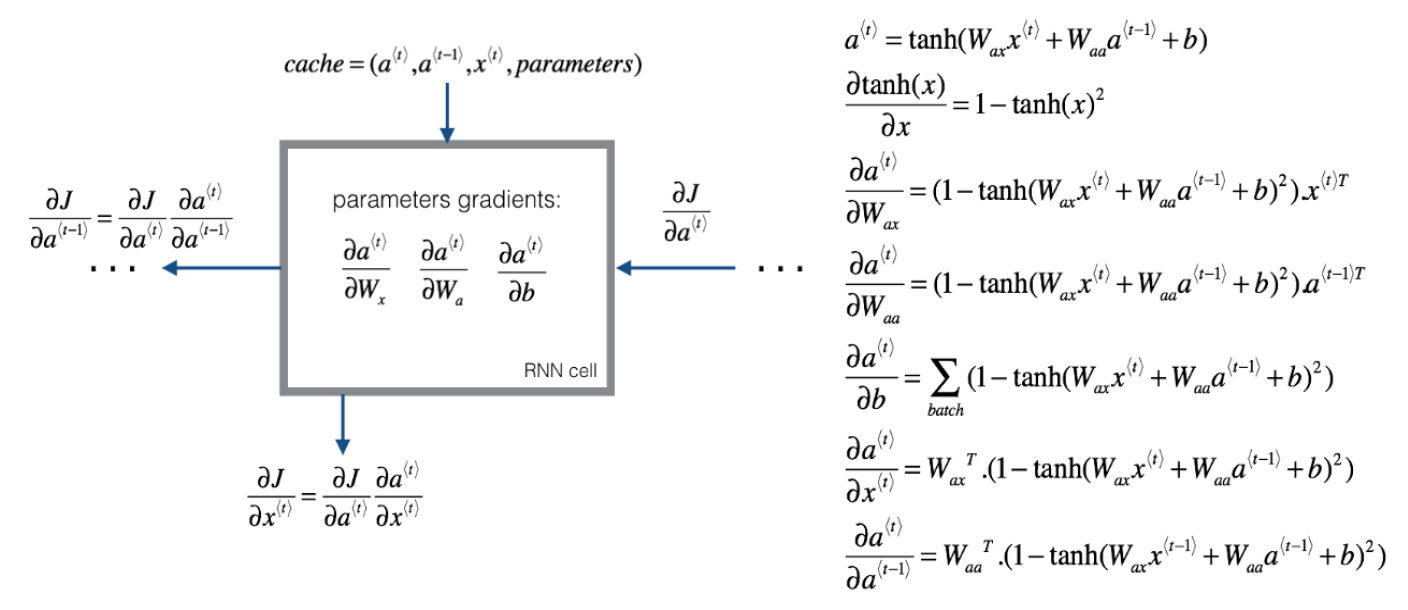
上述内容都是基于命名实体识别这个任务的,针对不同的任务,有多种不同的RNN结构,我们来看一下:
-
一对一
就是一个标准类型的神经网络
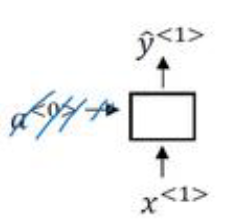
-
一对多
例如音乐生成,输入数字或者为空,即可得到一段音乐
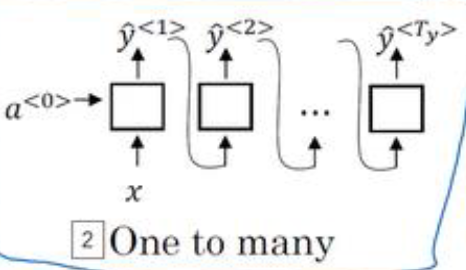
-
多对一
情感分类问题,输入一条评论,输出一个数字,代表情感的类型
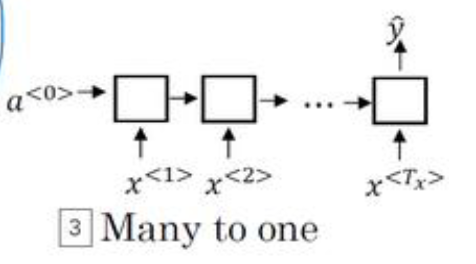
-
多对多-1
之前讨论的命名实体识别问题,每个单词对应一个输出
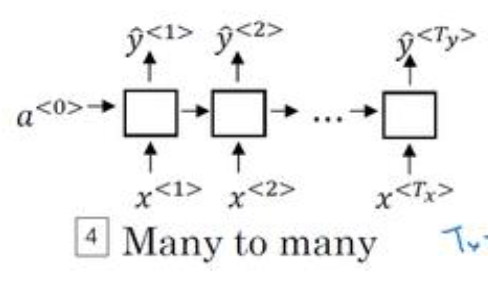
-
多对多-2
机器翻译任务,输入和输出不同。这种网络有两个部分,分为编码器和解码器。
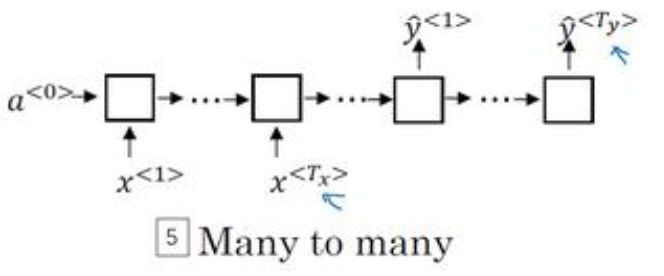
3. 语言模型
首先提出疑问,什么是语言模型呢,简单地说,语言模型会告诉我们某个特定的句子出现的概率是多少。
语言模型是两种系统的组成部分,一个是语音识别系统,另一个是机器翻译系统。
语言模型的输入是一个句子(一个文本序列),语言模型会估计序列中各个单词出现的概率(可能性)。
下面我们来具体看一下如何构建语言模型:
首先我们需要一个训练集,即一个很大的语料库(corpus),语料库是NLP的专有名词,指代很多或者很长的英文(或其他语言)句子组成的文本。
有了训练集之后,我们从训练集中抽取一个样本,即一个句子,我们首先需要对句子标记化,即先建立一个词典,然后根据单词的索引,把每个单词转换成one-hot向量,记得在句子的末尾处使用EOS进行标记。对于一些不在词典中的单次,我们使用UNK进行标记。
完成标志化之后,我们需要构建一个RNN来进一步构建文本序列的概率模型。
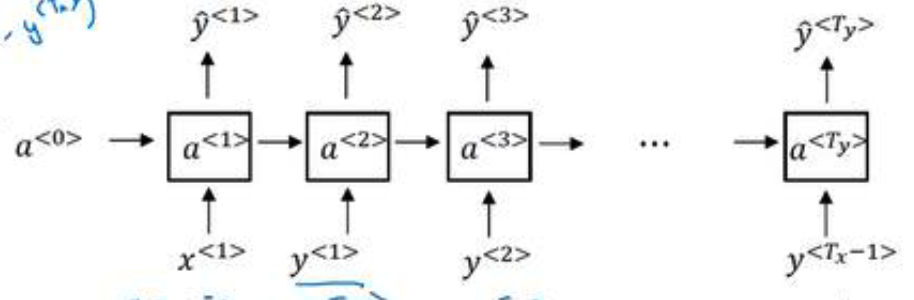
如上图所示,在第一个时间步,我们的输入$x^{<1>}=0,a^{<0>}=0$,输出为使用softmax对$a^{<1>}$进行一些预测,预测第一个词是什么,结果就是$\hat y^{<1>}$,表示所有词典中所有词出现的概率。在第二时间步,我们使用 $y^{<1>}$作为$x^{<2>}$作为输入,表示考虑到第一个词的情况下,第二个词的概率;第三时间步同样如此,不断迭代,直至最后$\hat y^{
为了训练当前网络,我们需要定义损失函数,单个时间步的损失函数为softmax的损失函数:
\[L^{<t>}(\hat y^{<t>},y^{<t>})=-\sum_i y_i^{<t>}\log \hat y_i^{<t>}\tag{3-1}\]总体损失函数就是把所有单个预测的损失函数相加:
\[L(\hat y,y)=\sum_t L^{<t>}(\hat y^{<t>},y^{<t>})\tag{3-2}\]我们使用我们的语料库训练这个RNN网络,训练完毕后,我们使用我们的语言模型进行预测:
现在有一个新句子,它是$y^{<1>}、y^{<2>}、y^{<3>}$,我们需要使用语言模型计算出这个句子出现的概率,计算方法为:
\[P(y^{<1>},y^{<2>},y^{<3>})=P(y^{<1>})P(y^{<2>} \mid y^{<1>})P(y^{<3>}\mid y^{<1>},y^{<2>})\tag{3-3}\]$P(y^{<1>})$即是第一个softmax层输出的结果;$P(y^{<2>} \mid y^{<1>})$是第二个softmax层输出的结果,代表考虑了$y^{<1>}$的情况下;$P(y^{<3>}\mid y^{<1>},y^{<2>})$是第三个softmax层输出的结果,代表考虑了$y^{<1>}$与$y^{<2>}$的情况下。
通过上述的学习,我们已经建立并训练好了一个RNN语言模型,但是我们想要知道我们的模型到底学到了什么,一种实用的办法就是进行一次新序列采样。具体做法如下:
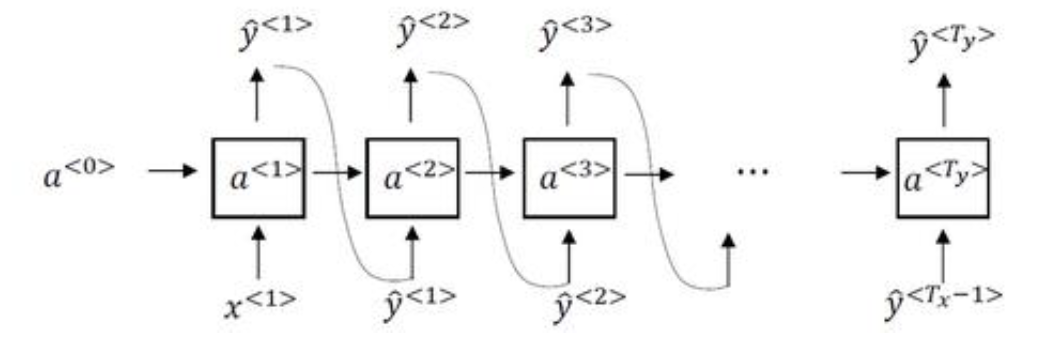
上图就是对新序列采样的整体流程示意图。我们首先根据$x^{<1>}=0,a^{<0>}=0$作为输入,经过softmax层后得到所有词语的概率,然后根据概率分布进行随机采样,然后进行下一时间步,将本次时间步随机采样的词语作为输入,得到下一时间步softmax层处理后的概率分布;不断执行上述迭代过程,一直到最后一个时间步。
判断最后一个时间步的方法有以下两种:
- 一直采样知道得到EOS标识
- 词典中没有EOS,需要规定最长的长度
我们构建的实际上是基于词汇的语言模型,我们还可以根据需求构建基于字符的语言模型:
顾名思义,基于字符的语言模型代表我们的字典中只有a-z的字母,还可以有0-9的数字,需要区分大小写,也可以加上每个字符的大小写,这些就是字典中的实际内容。这样我们构建的RNN语言模型中,每个时间步的输入不是一个one-hot的词语,而是one-hot的字母或数字。
基于字符的语言模型的优点有:
- 不必担心出现位置的标识,即任何短语都可以通过字符组成
缺点:
- 会得到太长的序列,因为每个时间步仅生成一个单词
- 捕捉句子前后的依赖关系时不如基于词汇的语言模型
- 计算成本高
4. RNN的梯度消失
在前面,我们学习了如何使用RNN模型实现命名实体识别与语言模型,但是RNN这个网络还有一个很大的问题,就是梯度消失。

上图表示语言模型中的RNN模型,实际上RNN并不擅长捕获长期依赖效应。在标准网络,我们讨论了梯度消失的问题,即在一个很深很深的网络中,先做前向传播再做反向传播,从输出得到的梯度很难传播回去,很难影响到靠前的权重,很难影响到前面层的计算。
这种问题在RNN中同样出现,因为梯度消失的问题,后面层的输出误差很难影响到前面层,基本的RNN模型会受到很多局部影响,即当前时间步的计算收到附近时间步的影响,因此对于靠前层的计算,很难影响到后面的层。
记得在讨论很深很深的标准网络时,也提到了梯度爆炸,但是梯度消失是RNN中的主要问题,因为梯度爆炸在RNN中出现的话就会很容易观察到。因为出现梯度爆炸时,我们的参数会大到崩溃,会出现Nan或者不是数字的情况,意味着我们的网络出现了数值溢出。
如果出现了梯度爆炸,我们可以使用梯度修剪。梯度修剪的意思是观察我们的梯度向量,如果他大于某个阈值,我们可以缩放梯度向量,保证不会太大。然后梯度消失很难解决。
下面我们介绍一种方法,它可以改善梯度消失问题,改变了RNN的隐藏层,使其可以更好地捕捉深层连接,它就是门控循环单元(GRU)。
上图是RNN影藏层单元的可视化,根据这个图,我们将其改造成GRU。
GRU有一个新的变量c,即记忆细胞,提供记忆的能力,在时间t处,提供记忆细胞$c^{
GRU输出的激活值为$a^{
同时,我们需要使用sigmoid计算出一个更新门,即$\Gamma_u$:
\[\Gamma_u=\sigma(W_u[c^{<t-1>}+x^{<t>}]+b_u)\tag{4-2}\]$c^{
通过上述公式,我们就获取了当前时间步的记忆细胞,对应着标准RNN的$a^{
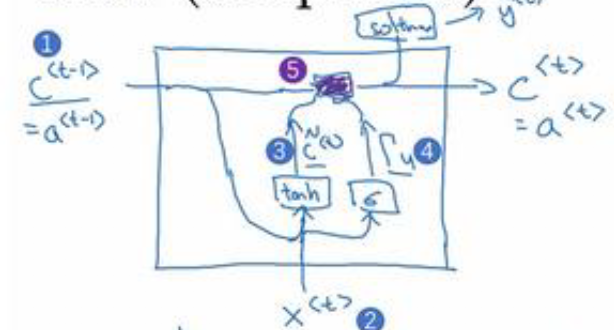
上述GRU单元我么可以理解为一个简化的GRU单元,其主要思想是通过一个门控制。当我们从左导入输入一个句子的时候,在每个时间步,由门决定更新当前记忆细胞还是不更新,如果不更新$\Gamma_u=0$,或者说非常接近0。这种情况下,$c^{
下面我们来看一下完整的GRU单元:
完整的GRU需要再添加一个门$\Gamma_r$,代表相关性的门。他需要一个新的参数矩阵$W_r$来计算:
\[\Gamma_r=\sigma(W_r[c^{<t-1>}+x^{<t>}]+b_r)\tag{4-4}\]然后我们使用计算的$\Gamma_r$门参与计算$ \tilde c^{
这就是复杂版本的GRU相对于简单版本增加的内容。
我们来思考为什么复杂版本要增加$\Gamma_r$门,因为很多年来研究者们试验过很多不同的方法设计这些单元,尝试让神经网络有着更深层的连接,尝试产生更大范围的影响,同时解决梯度消失问题。完成的GRU就是最常用的一个版本,以为在很多问题上是非常健壮和实用的。但是GRU的简化版本也很常用。
GRU可以在一定程度上解决梯度消失问题,我们来看另一个模型,他同样可以让模型在序列中学习非常深的链接,即长短时记忆神经网络(LSTM)。
我们首先回忆一下GRU每个时间步的处理过程:
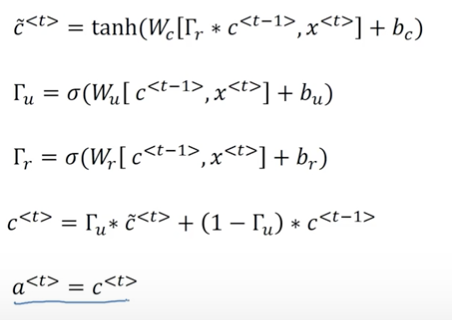
在GRU中,我们使用两个门控单元,更新门$\Gamma_u$和相关门$\Gamma_r$,且$a^{
LSTM是一个比GRU更加强大和通用的版本:
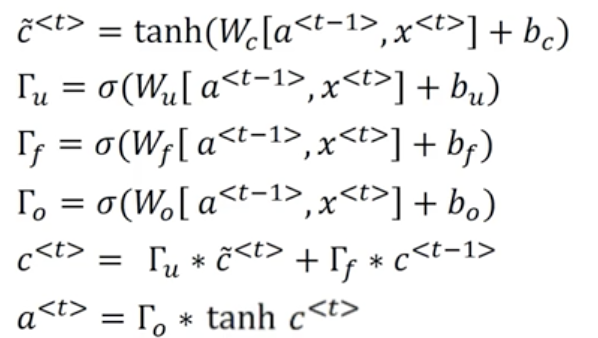
上图就是LSTM时间步的计算过程,其中$\tilde c^{
对比GRU门控单元,LSTM的计算过程很容易理解,我们看一下LSTM的示意图:
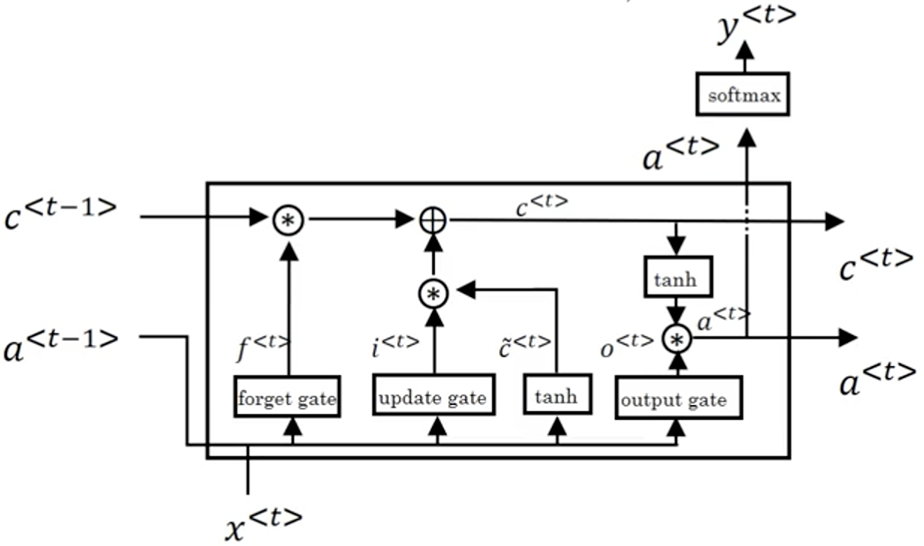
上述示意图就是LSTM的内部流程,虽然看起来很复杂,但是仍然是之前的计算公式。
LSTM是非常容易把$c^{<0>}$的值传到最后一个时间步内,这也是LSTM与GRU为什么擅长长时间记忆某个值,即使经过很长很长时间。
LSTM还有一些其他的版本。例如门值不仅取决于$a^{
GRU的优点:
- 相比于LSTM更加简单,因此更容易创建一个更大的网络
- 只有两个门,在计算性上运行的更快
LSTM优点:
- 有三个门,更加强大
一般来说会选择LSTM,但是在特殊情况下,例如很复杂的网络,GRU也会被选择到。
5. 双向循环神经网络(Bidirectional RNN)
在了解基本RNN与其变体之后,我们了解一下双向RNN网络,它不仅可以让我们在序列的某点处获取之前的信息,还可以获取未来的信息。
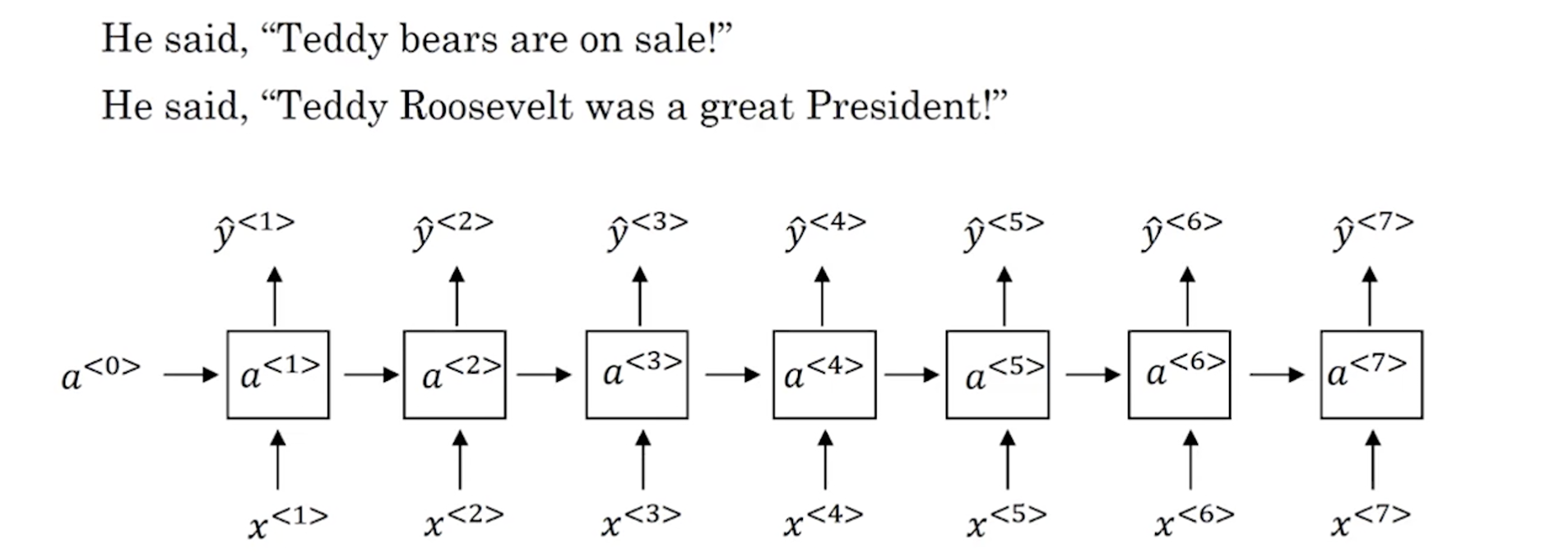
这是最开始我们研究的命名实体识别任务,加入我们需要判断Teddy是否是一个人名,仅仅看前面的信息是不够的,我们需要更多的信息,上图中显示的是非双向的RNN,这些单元可以使标准RNN,也可以是GRU,或者LSTM。
双向RNN需要我们首先从左到右前向传播计算每个时间步的激活值,我们使用$\overrightarrow a^{<1>}、\overrightarrow a^{<2>}、\overrightarrow a^{<3>}、\overrightarrow a^{
上述步骤完成后,我们从右到左前向传播计算每个时间步的激活值,我们使用$\overleftarrow a^{<1>}、\overleftarrow a^{<2>}、\overleftarrow a^{<3>}、\overleftarrow a^{
在所有激活值计算完成后,我们就可以预测结果了,我们使用公式:
\[\hat y^{<t>}=g(W_y[\overrightarrow a^{<t>},\overleftarrow a^{<t>}]+b_y)\tag{5-1}\]使用上述公式计算每个时间步的预测结果。所以预测结果不仅考虑到了前面的$x^{<1>}、x^{<2>}$的信息,同样也会考虑反向的$x^{<6>}、x^{<7>}$等的信息,相当于同时考虑了现在和未来的信息。
以上就是双向RNN的内容,在双向RNN中,这些基本单元不仅仅是标准RNN单元,也可以是GRU单元或者LSTM单元,在NLP中使用非常广泛。
双向RNN的缺点就是需要完成的数据序列,例如在语音识别中,我们需要等待某个人把话说完才能预测,但是这一般不是问题。
6. 深层循环神经网络(Deep RNNs)
如果我们要学习非常复杂的函数,通常我们会把RNN的多个层堆叠在一起构建更深的模型。
其实RNN的堆叠过程和标准神经网络的堆叠过程很像,我们看一下堆叠后的结构,然后进行分析:
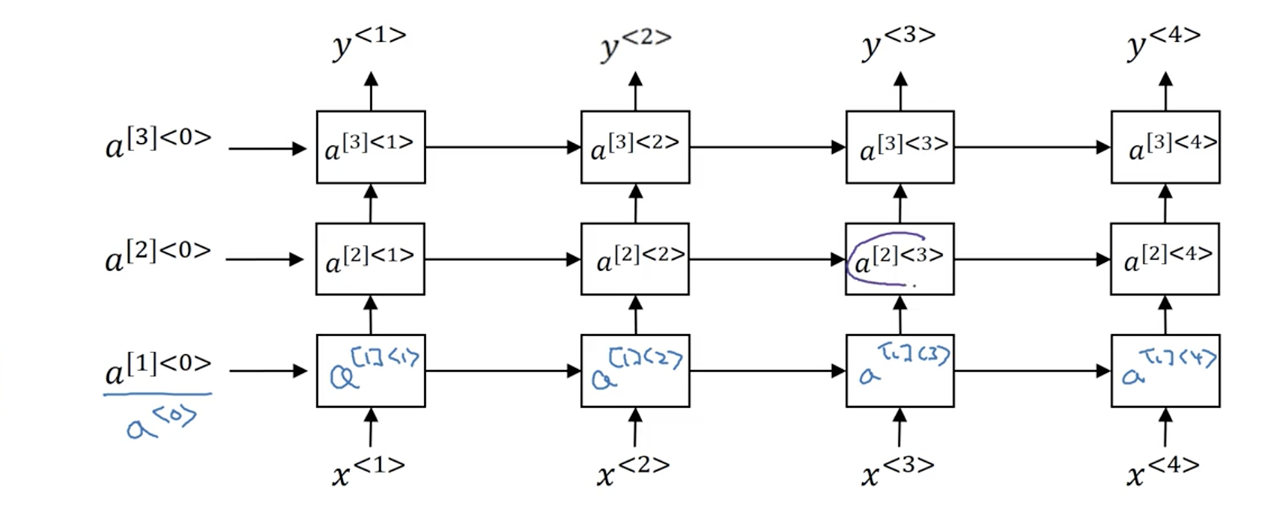
如上图所示,第一层为标准的RNN网络,第二层叠加在第一层之上,仍然是RNN网络,第三层同样如此。这样堆叠后,我们的网络中的单元是怎样计算的呢?
我们看一下激活值$a^{[2]<3>}$的计算:
\[a^{[2]<3>}=g(W^{[2]}_a[a^{[2]<2>},a^{[1]<3>}]+b_a^{[2]})\tag{6-1}\]其中[2]代表第二层中的参数。
对于标准神经网络,我们见过很深的网络,甚至包括100层,但是对于RNN来说,3层就已经很多了。由于时间的维度,即使只有很少的几层,RNN的网络都会变得很大。但是包含RNN的很深的层我们可以见到这种:将RNN的输出堆叠很多FC,他们在同一层并不连接。
对于上面的深层RNN中的单元,可以使标准RNN单元,也可以是GRU单元或者是LSTM单元。